Kótované promítání se mimo jiné využívá k teoretickému řešení střech. Pro jednoduchost budeme řešit střechy tvořené částmi rovin stejného spádu, tj. všechny roviny mají stejnou odchylku od průmětny. Vodorovnou rovinu, v níž leží okapy, ztotožníme s průmětnou. Střechu budeme zadávat jejím půdorysem. Jako půdorys střechy budeme pro jednoduchost volit obdélník nebo kombinaci obdélníků s rovnoběžnými stranami (viz např. obr. 38). Principy teoretického řešení střech tvořených částmi rovin stejného spádu lze však uplatnit i u složitějších nepravoúhlých půdorysů.

Úsečky na obvodu půdorysu určují stopy jednotlivých rovin, které v řešení použijeme. Řešit střechy znamená najít průsečnice těchto rovin. Pokud jsou jejich stopy různoběžné, jejich průsečnice se zobrazí jako osy úhlů daných jejich stopami (obr. 36). Pokud jsou stopy těchto rovin rovnoběžné, jejich průsečnice se zobrazí jako osy pásů rovnoběžek daného jejich stopami (obr. 37).

Na stranách mnohoúhelníku ležícího ve vodorovné rovině, jehož půdorys je půdorysem budovy, se střecha opírá o vodorovnou rovinu. Těmto stranám se říká římsové hrany střechy. Průsečné hrany rovin s různoběžnými stopami nazýváme úžlabí, pokud voda stéká po střeše směrem k této hraně, nebo nároží, pokud voda stéká po střeše směrem od této hrany. Vodorovné nároží nazýváme hřeben (obr. 39). Vodorovné úžlabí nazýváme žlab. Žlabu se zásadně vyhýbáme, protože by se v něm voda shromažďovala a špatně by ze střechy odtékala.

V příkladech je z praktických důvodů vhodné si roviny částí střech očíslovat. Tedy u každé stopy napíšeme číslo roviny, do které patří. Dále průsečnice rovin také očíslujeme podle rovin, kterým náleží. Průsečnici rovin 1 a 2 například označíme 12. Pro lepší představu o tvaru střechy také šipkami vyznačíme směr spádu střechy.

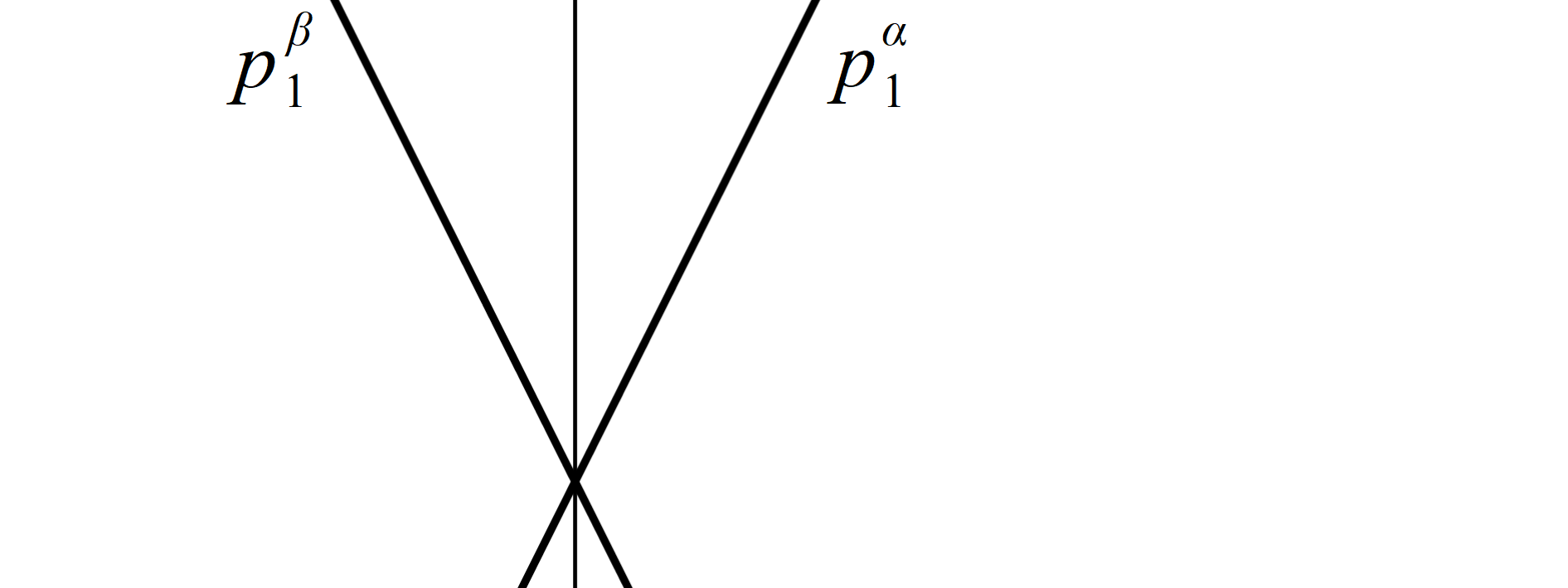
Obr. 36

Obr. 37

Obr. 38: Půdorys střechy

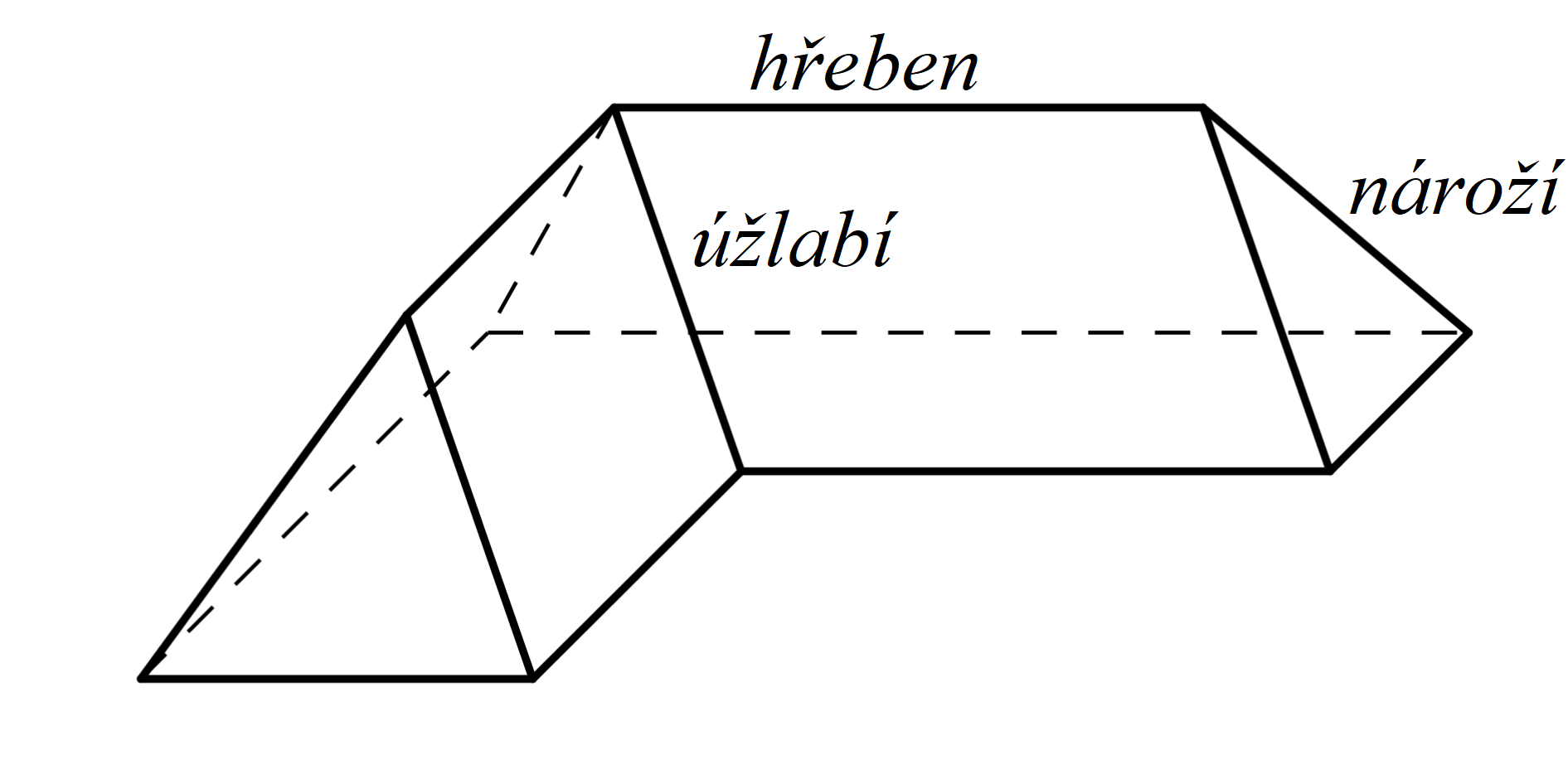
Obr. 39: Prostorový náhled na střechu