Určete vzájemnou polohu přímek a a b. Pokud jsou různoběžné, určete jejich průsečík.
a = ↔AB, A = [1; 1; 1], B = [3; 3; 5]
b = ↔CD, C = [2; 2; 2], D = [6; 6; −1]
Řešení (obr. 17)
Průměty přímek a, b jsou totožné přímky. Přímky a, b tedy leží v jedné promítací rovině a jsou buď různoběžné nebo rovnoběžné. Abychom mohli určit vzájemnou polohu těchto přímek, musíme sklopit jejich promítací rovinu. Přímky (a), (b) jsou různoběžné, a proto jsou přímky a, b různoběžné. Ve sklopení vidíme sklopený průsečík E přímek a, b. Pata kolmice vedená tímto bodem k přímce a1 = b1 je bod E1. Kóta zE bodu E je kladná a je rovna vzdálenosti bodů E1, (E).
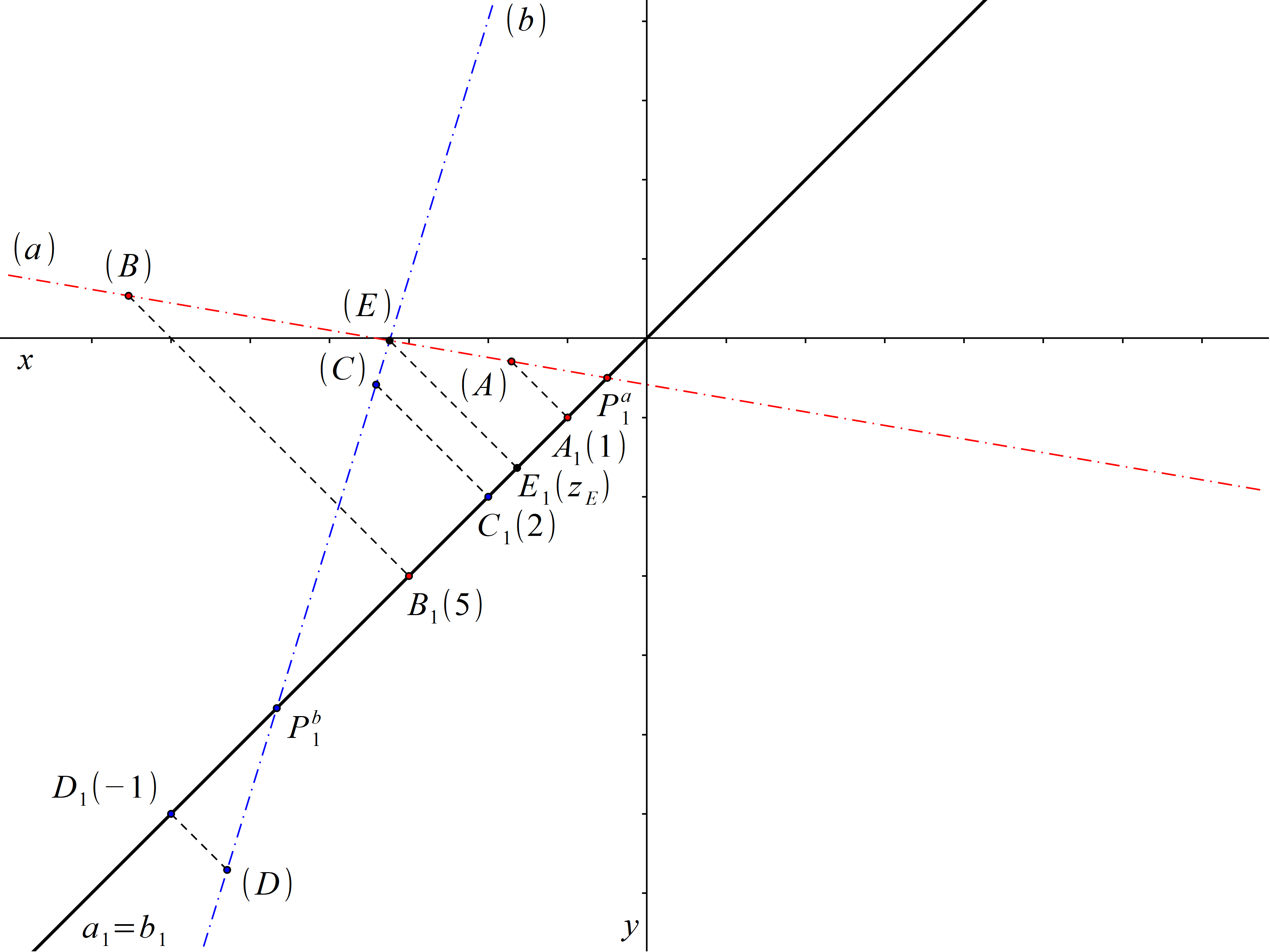
Obr. 17: Řešení příkladu 4.8
