Určete vzájemnou polohu přímky a a roviny α. Pokud jsou různoběžné, určete jejich průsečík.

α = ↔ABC, A = [8; 6; 0], B = [6; 7; 0], C = [6; 5; 2]

a = ↔DE, D = [2; 5; 2], E = [8; 9; 8]

Řešení (obr. 22)

Body A, B leží v průmětně, proto určují stopu roviny α. Přímka \( h ^\alpha_1 \) rovnoběžná se stopou roviny α vedená bodem C₁ je průmětem hlavní přímky h^α roviny α o kótě 2. Rovina α není promítací a přímka a také ne. Přímka a a rovina α tedy mohou být různoběžné i rovnoběžné. V takovém případě si pomůžeme krycí přímkou q, pro kterou platí, že q₁ = a₁ a q ⊂ α. Přímka q protíná hlavní přímku h^α v bodě F o kótě 2 a stopník P^q přímky q leží na stopě roviny α. Sklopíme promítací rovinu přímek a, q. Přímky (a), (q) jsou různoběžné a protínají se v bodě (G). Z toho plyne, že přímky a, q jsou různoběžné a protínají se v bodě G. Přímka a je tedy různoběžná s rovinou α a průsečík G přímek a, q je zároveň průsečíkem přímky a a roviny α. Kóta bodu G je kladná a je rovna vzdálenosti bodů G₁, (G).

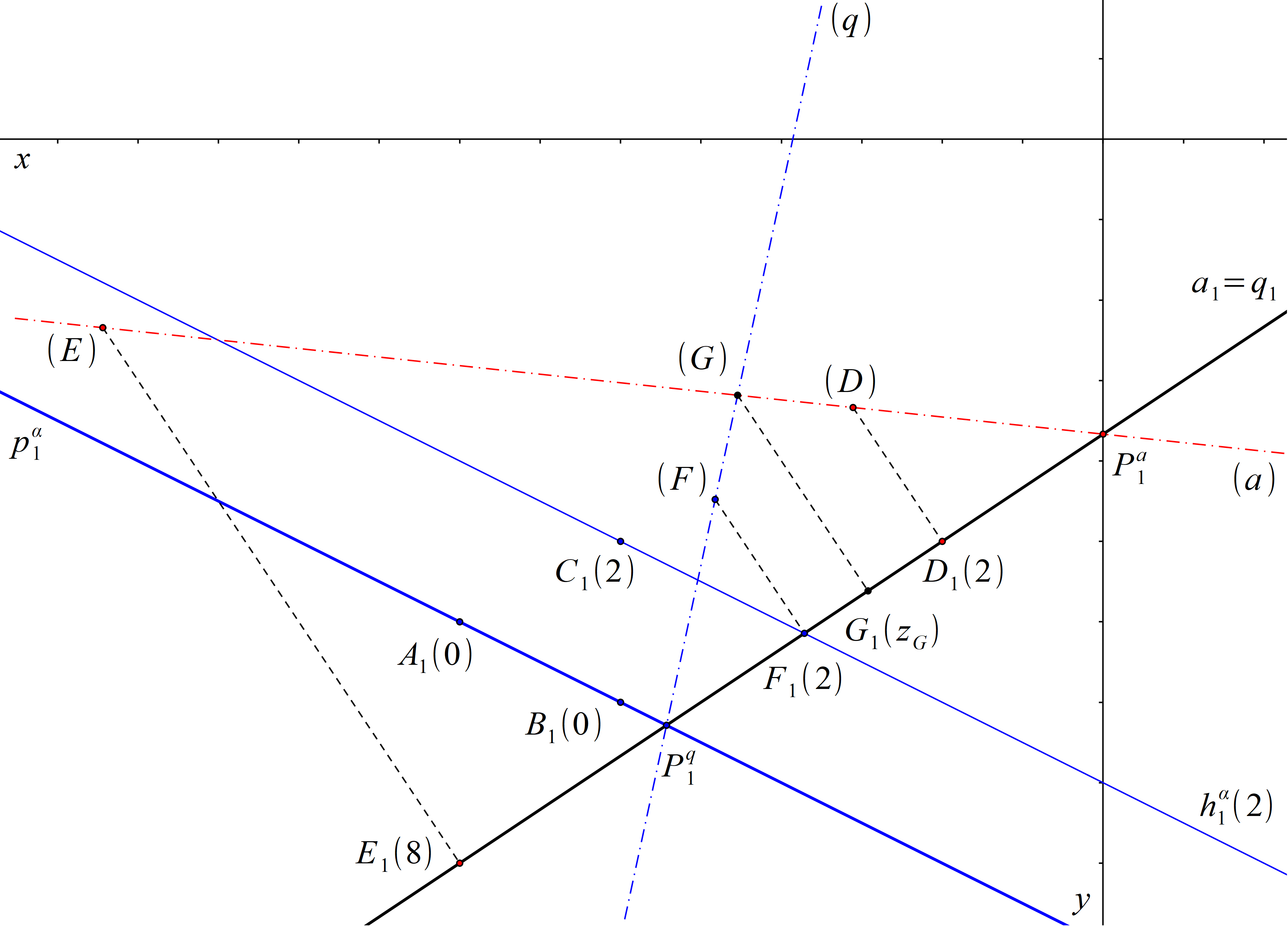
Obr. 22: Řešení příkladu 6.1

Krokovaná konstrukce

Předchozí příklad

Následující příklad

Teorie k příkladu