Přesvědčte se, že jsou roviny α a β rovnoběžné, a určete jejich vzdálenost.
α = ↔ABC, A = [9; 5; 0], B = [−4; 0; 0], C = [3; 1; 2]
β = ↔DEF, D = [10; 9; 0], E = [5; 4; 0], F = [5; 8; 4]
Řešení (obr. 81)
Nejprve se přesvědčíme o rovnoběžnosti zadaných rovin. Stopy rovin α a β jsou rovnoběžné, roviny α a β mohou tedy být rovnoběžné nebo různoběžné (viz kapitola Vzájemná poloha dvou rovin). Vzájemnou polohu rovin α a β zjistíme sklopením promítací roviny σ kolmé ke stopám rovin α a β. V této promítací rovině leží spádová přímka sα roviny α a spádová přímka sβ roviny β. Přímku (sα) sestrojíme pomocí známého stopníku a bodu G o kótě 2. Přímku (sβ) sestrojíme pomocí známého stopníku a bodu H o kótě 4. Přímky (sα) a (sβ) jsou rovnoběžné, tudíž jsou roviny α, β rovnoběžné.
Vzdálenost rovin α a β je rovna vzdálenosti libovolného bodu roviny β od roviny α. Určeme nyní vzdálenost daných rovin jako vzdálenost bodu H od roviny α. Bodem H vedeme kolmici a k rovině α a najdeme průsečík I přímky a s rovinou α. Hledaná vzdálenost je rovna délce úsečky HI. Přímka a leží v promítací rovině σ. Ve sklopení této promítací roviny sestrojíme přímku (a) jako kolmici vedenou bodem (H) k přímce (sα). Průsečík přímek (a) a (sα) je sklopeným průsečíkem I přímky a a roviny α. Hledaná vzdálenost rovin α a β je rovna délce úsečky (H)(I).
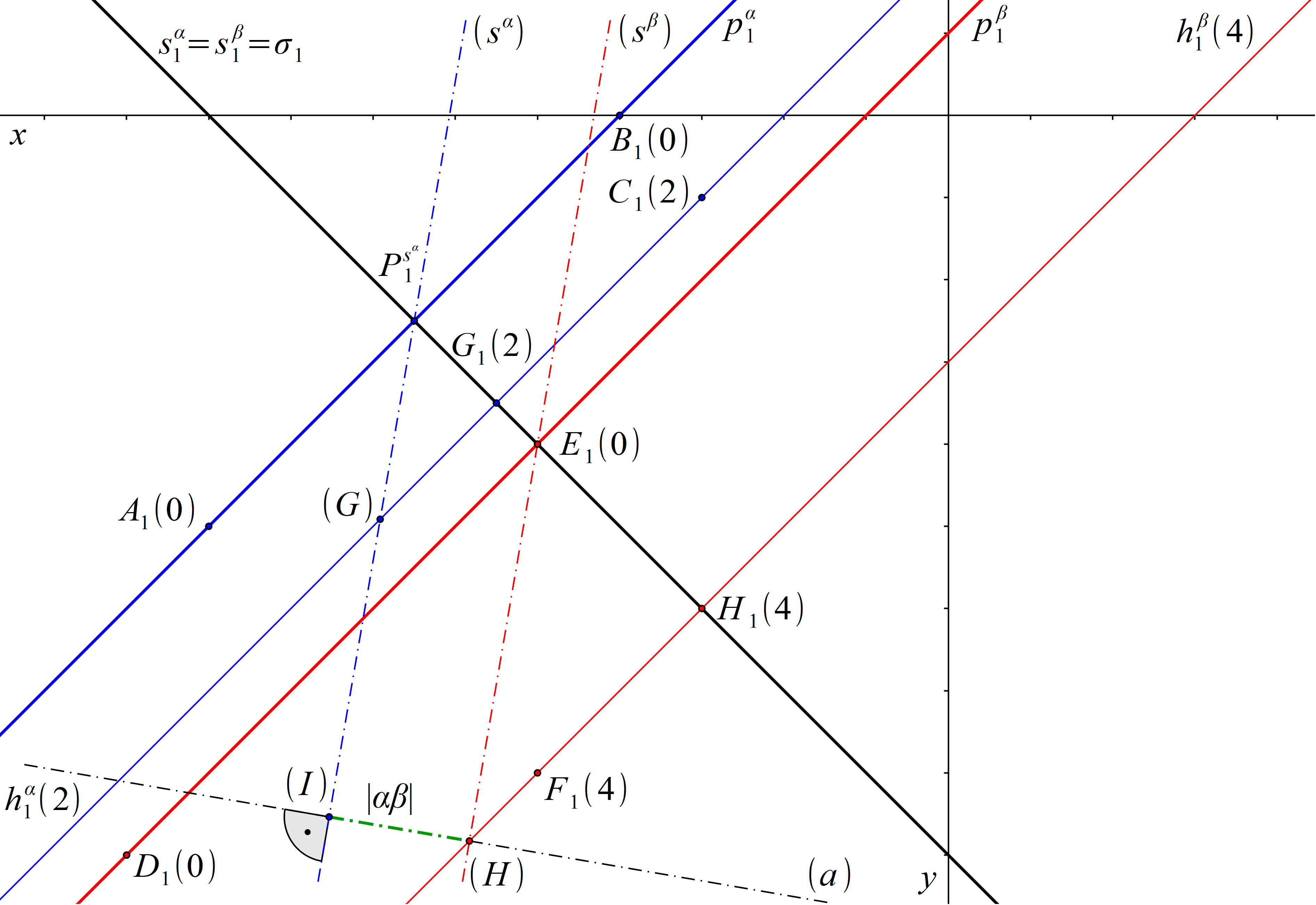
Obr. 81: Řešení příkladu 16.3
