Určete vzdálenost bodu D = [5; 3; 6] od roviny α.
α = ↔ABC, A = [10; 5; 0], B = [8; −1; 0], C = [1; 2; 4]
Řešení (obr. 80)
Jelikož body A, B leží v průmětně, určují stopu roviny α. Abychom zjistili vzdálenost bodu D od roviny α, najdeme pravoúhlý průmět E bodu D do roviny α (stejným způsobem, jako v příkladu 12.3). Bod E je patou kolmice b vedené bodem D k rovině α. Přímka b1 prochází bodem D1 kolmo ke stopě roviny α a splývá s průmětem \(s^\alpha_1 \) spádové přímky sα roviny α. Ve sklopení promítací roviny společné přímkám b a sα sestrojíme spádovou přímku (sα), a to pomocí známého stopníku \( P^ {s^\alpha }\) a průsečíku G spádové přímky s hlavní přímkou o kótě 4. Dále v tomto sklopení sestrojíme přímku (b), která prochází bodem (D) a je kolmá k přímce (sα). Průsečík (E) přímek (sα) a (b) je sklopeným pravoúhlým průmětem E bodu D do roviny α. Hledaná vzdálenost bodu D od roviny α je rovna vzdálenosti bodů (E) a (D).
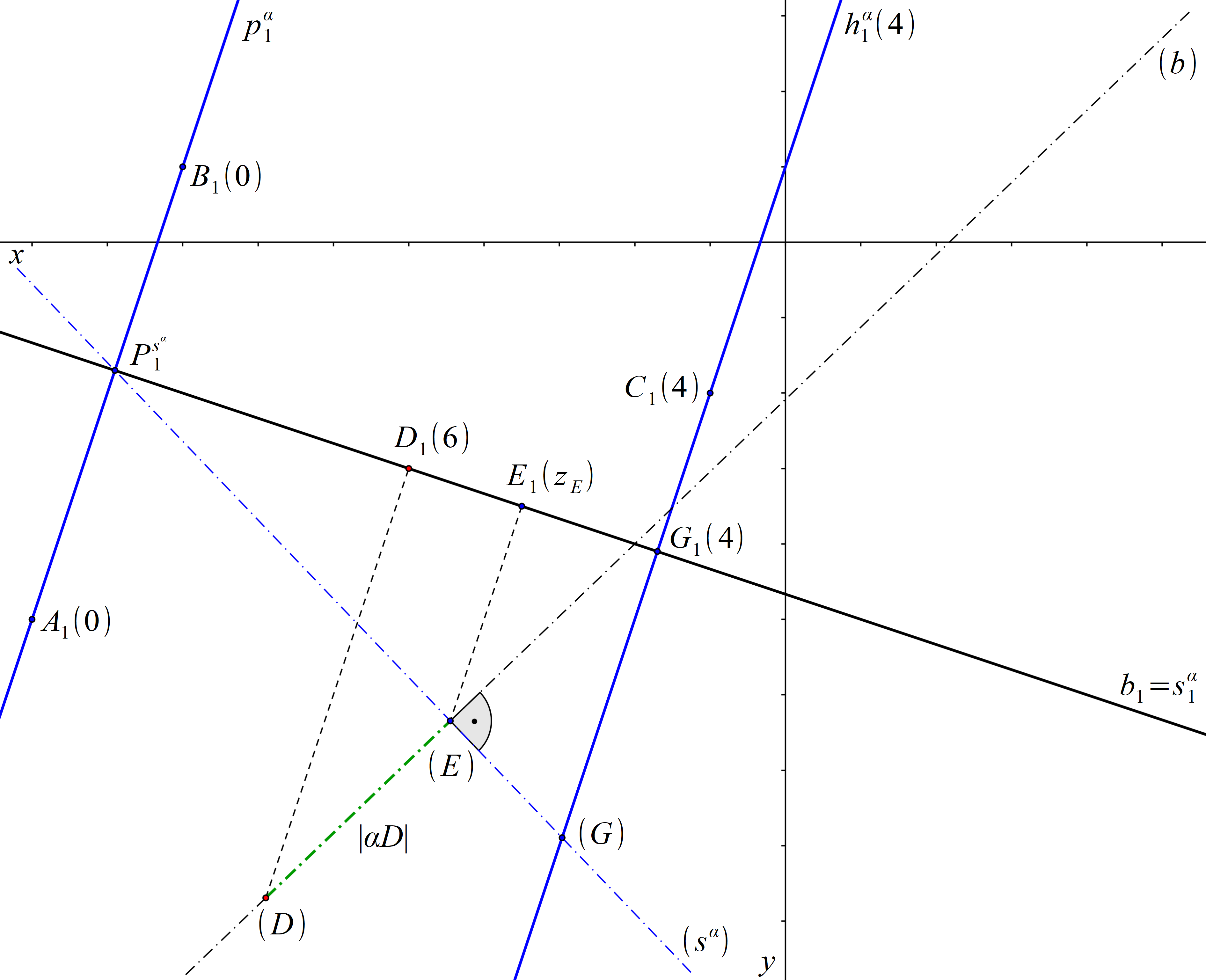
Obr. 80: Řešení příkladu 16.2
