Určete kótu bodu C tak, aby ležel na přímce a.
a = ↔AB, A = [1; 2; 3], B = [4; 4; 1], C = [2; ?; ?]
Řešení (obr. 8)
Nejdříve sestrojíme průměty A1 a B1 bodů A a B, které určí průmět a1 přímky a. Bod C1 najdeme jako průsečík přímky rovnoběžné s osou y jdoucí bodem 2 na ose x a přímky a1. Kótu bodu C zjistíme pomocí sklopení promítací roviny přímky a. Průsečíkem kolmice bodem C1 k a1 a přímky (a) je bod (C). Vzdálenost bodů C a (C) je absolutní hodnota hledané kóty bodu C. Protože bod (C) leží ve stejné polorovině určené přímkou a1 jako bod (A) a bod A má kladnou kótu, je kóta bodu C také kladná.
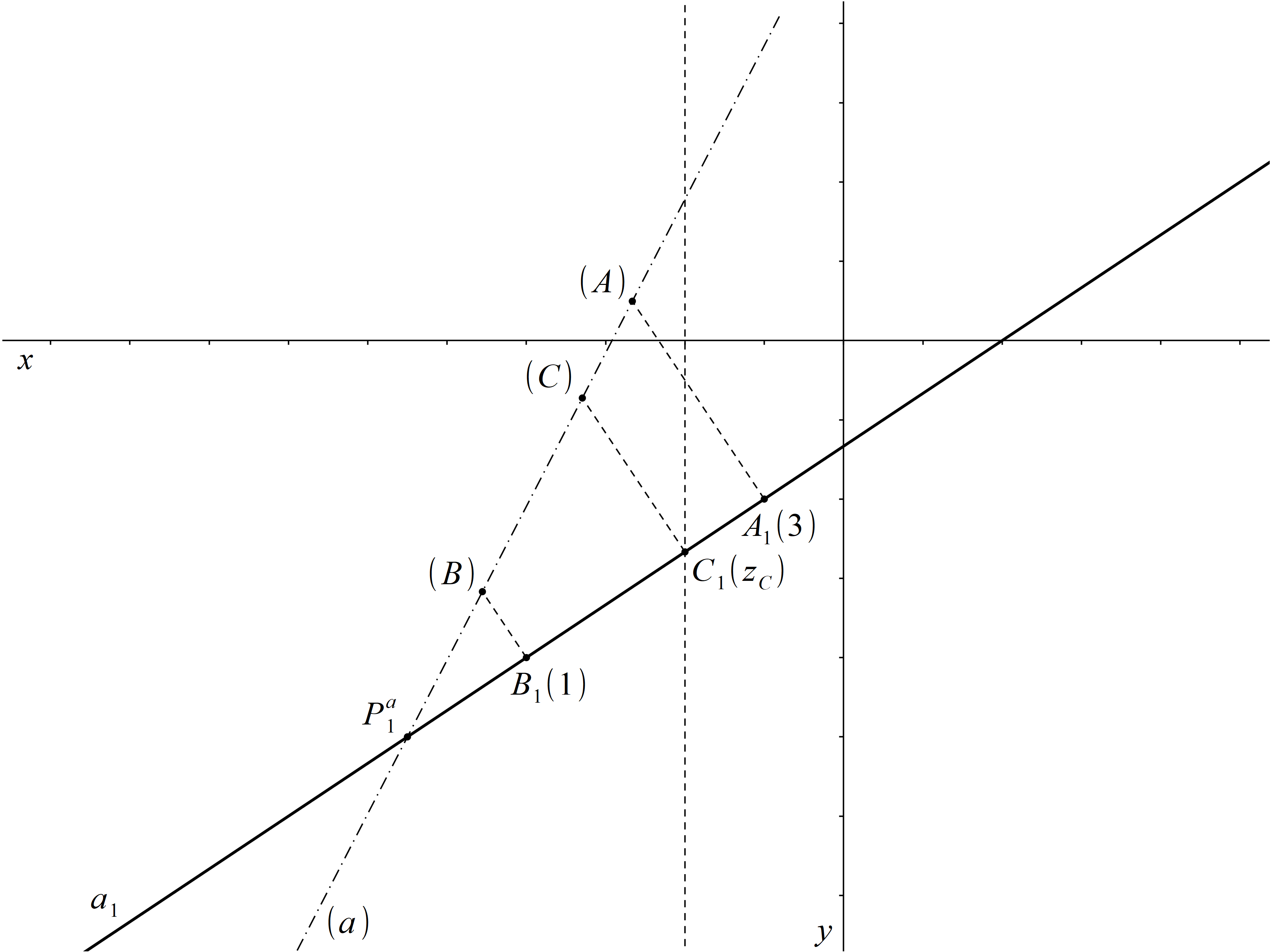
Obr. 8: Řešení příkladu 3.2
