Na přímce a určete bod C o kótě 3.
a = ↔AB, A = [2; 2; 1], B = [6; 4; 5]
Řešení (obr. 9)
Nejdříve sestrojíme průměty A1 a B1 bodů A a B, které určí průmět a1 přímky a. Dále sklopíme promítací rovinu přímky a. Sestrojíme pomocnou rovnoběžku s přímkou a1 ve vzdálenosti 3, a to ve stejné polorovině jako bod (A). Bod (C) je průsečíkem přímky (a) s pomocnou rovnoběžkou. Bod C1 najdeme jako patu kolmice vedené bodem (C) k a1.
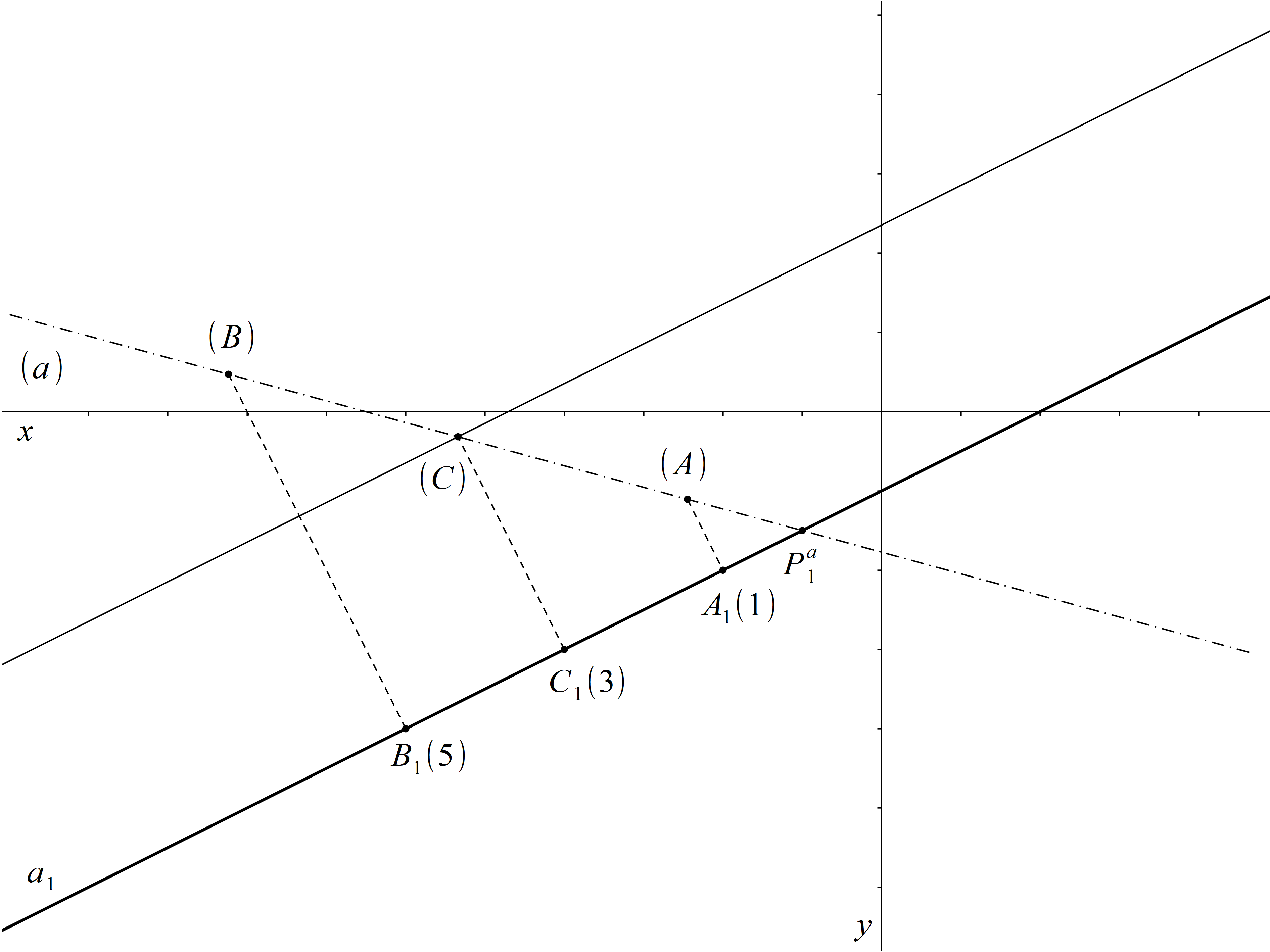
Obr. 9: Řešení příkladu 3.3
