Určete vzájemnou polohu přímek a a b. Pokud jsou různoběžné, určete jejich průsečík.
a = ↔AB, A = [2; 1; 1], B = [4; 5; 3]
b = ↔CD, C = [2; 4; 1], D = [5; 1; 4]
Řešení (obr. 12)
Průměty přímek a, b jsou různoběžné přímky. Přímky a, b jsou tedy různoběžné nebo mimoběžné. Průsečík přímek a1, b1 je průmětem bodů E a F, kde E Î a a F Î b. Pokud mají body E, F stejnou kótu, splývají. Přímky a, b jsou potom různoběžné. V opačném případě jsou mimoběžné. Kóty bodů E, F zjistíme pomocí sklopení promítacích rovin přímek a, b. Průsečíkem kolmice bodem E1 k a1 a přímky (a) je bod (E), průsečíkem kolmice bodem F1 k b1 a přímky (b) je bod (F). Nyní vidíme, že zE = |E1(E)| = zF = |F1(F)|, tudíž body E, F splývají. Přímky a, b jsou tedy různoběžné a protínají se v bodě E = F.
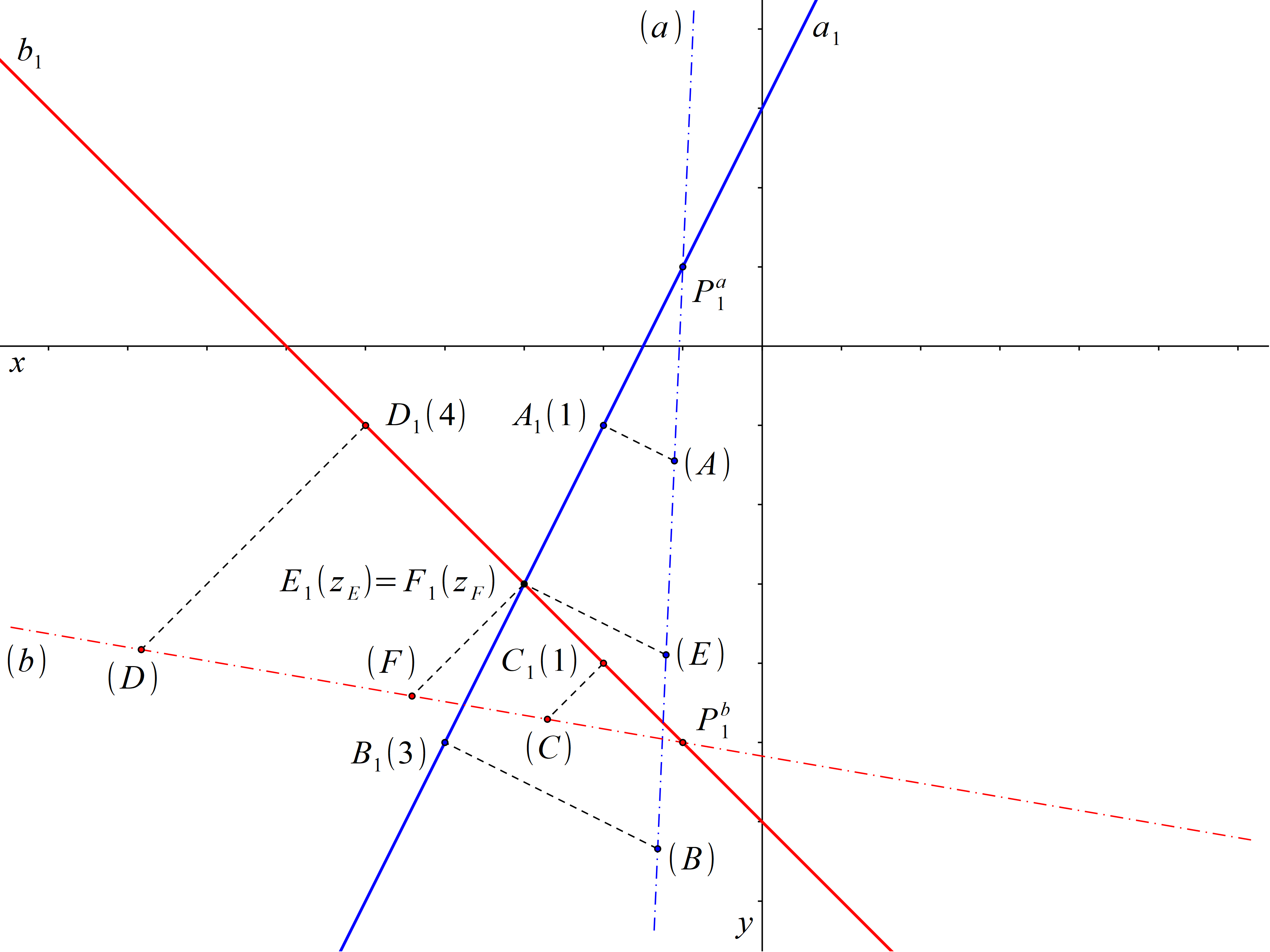
Obr. 12: Řešení příkladu 4.3
