Určete odchylku φ přímek a = ↔AB a b = ↔BC.
A = [11; 9; 0], B = [7; 3; 6], C = [2; 9; −1]
Řešení (obr. 54)
Průměty přímek a a b jsou různoběžné přímky a1 a b1, které se protínají v bodě B1. Protože bod B leží na obou přímkách, jsou přímky a a b různoběžné. Abychom určili odchylku přímek a a b, otočíme rovinu α danou těmito dvěma přímkami do průmětny. Nejprve zobrazíme stopu roviny α. Protože je kóta bodu A rovna nule, je bod A jedním bodem stopy roviny α. Dalším bodem stopy roviny α je stopník Pb přímky b, který určíme pomocí sklopení promítací roviny přímky b. Dále ve sklopení promítací roviny spádové přímky sα roviny α procházející bodem B sestrojíme bod (B) a kružnici otáčení (kB) bodu B, jejímž středem je stopník \( P^ {s^\alpha } \) přímky sα a jejímž poloměrem je vzdálednost bodu \( P^ {s^\alpha } \) od bodu (B). Bod B0 je průsečíkem přímky \( s^\alpha_1 \) a kružnice (kB). Přímka a0 je spojnicí bodu B0 a bodu A. Přímka b0 je spojnicí bodu B0 a bodu Pb. Odchylka φ přímek a a b v prostoru je rovna odchylce přímek a0 a b0.
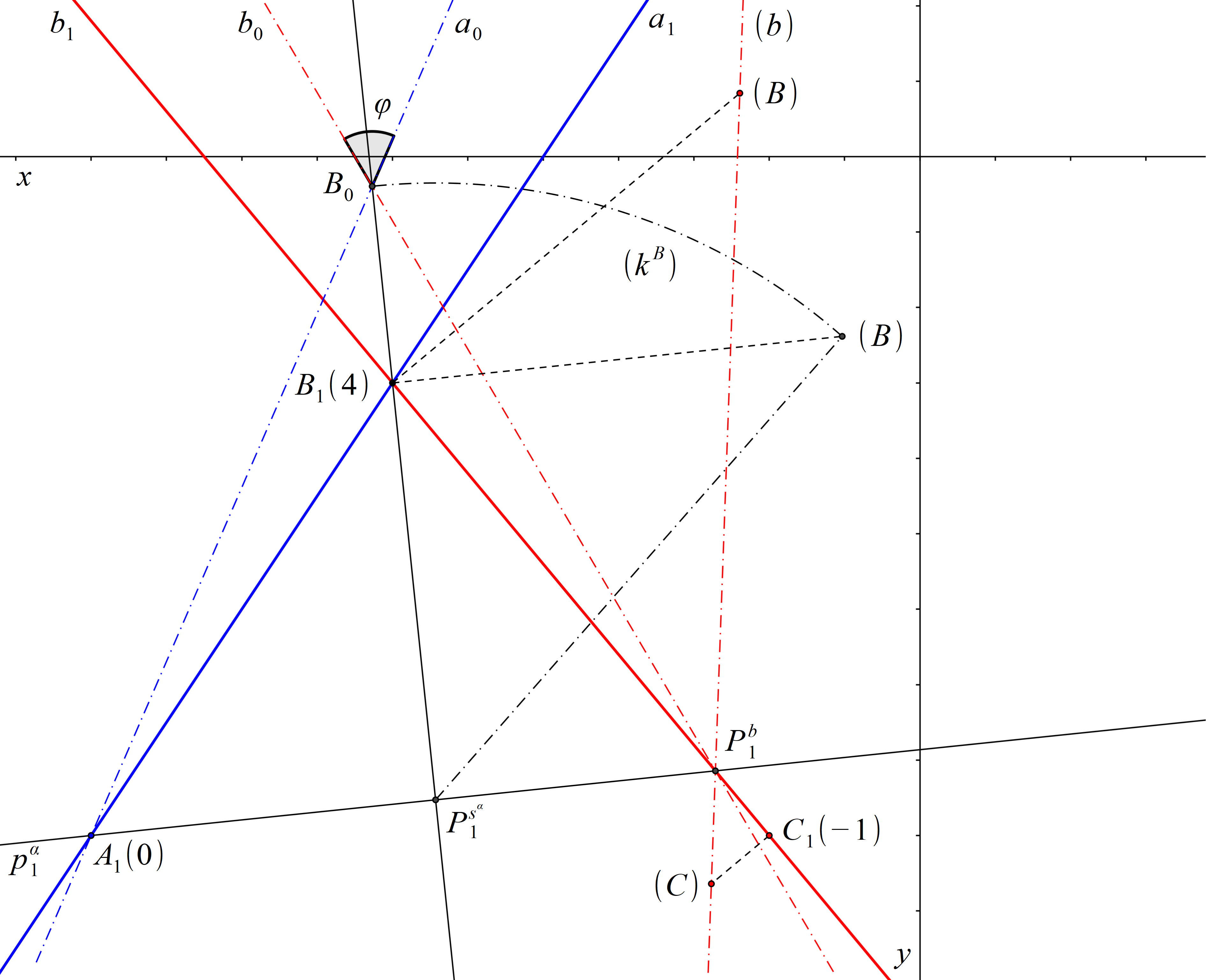
Obr. 54: Řešení příkladu 11.1
