Určete odchylku φ přímek a a b.
a = ↔AB, A = [11; 8; 1], B = [11; 8; 3]
b = ↔CD, C = [8; 5; 5], D = [6; 3; 3]
Řešení (obr. 55)
Z průmětů přímek a a b vidíme, že přímka a je kolmá k průmětně a leží v promítací rovině přímky b. Z toho plyne, že přímky a a b jsou různoběžné. Abychom určili odchylku φ přímek a a b, stačí sklopit promítací rovinu přímky b. Odchylka φ přímek a a b v prostoru je rovna odchylce přímek (a) a (b).
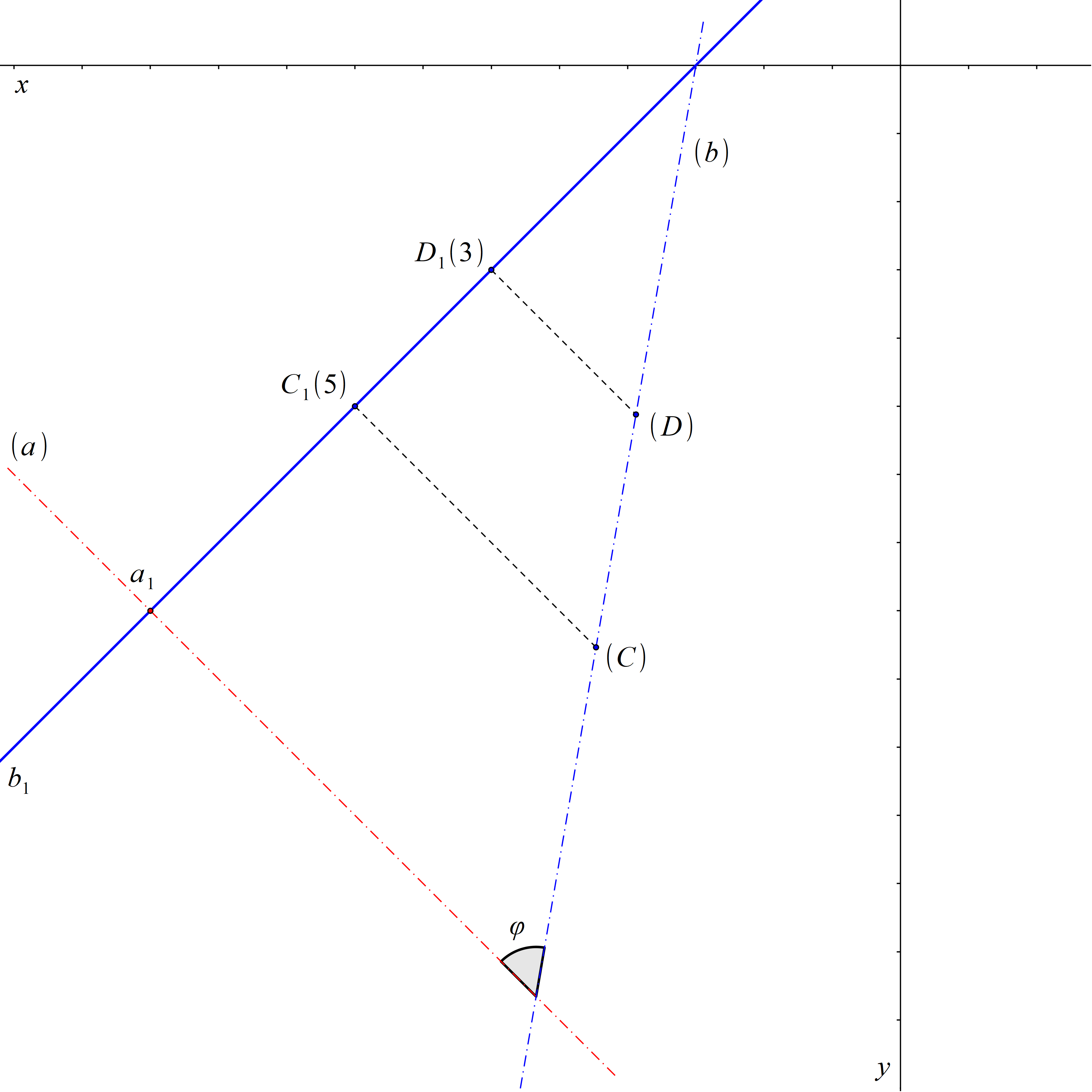
Obr. 55: Řešení příkladu 11.2
