Určete odchylku φ přímek a a b.
a = ↔AB, A = [9; 5; 0], B = [6; 2; 6]
b = ↔CD, C = [4; 5; 3], D = [2; 3; −2]
Řešení (obr. 59)
Průměty přímek a a b jsou rovnoběžné přímky a1 a b1. Nejprve zjistíme vzájemnou polohu přímek a a b, a to tak, že sklopíme jejich promítací roviny „na stejnou stranu“. V tomto případě jsou přímky (a) a (b) různoběžné, přímky a a b jsou tedy mimoběžné.
Abychom určili odchylku přímek a a b, vedeme libovolným bodem přímky a přímku \( \tilde{b} \) rovnoběžnou s přímkou b. Veďme nyní přímku \( \tilde{b} \) například bodem B. Přímky a a \( \tilde{b} \) potom leží v jedné promítací rovině, jejich průměty jsou totožné přímky. Odchylka přímek a a b je nyní rovna odchylce přímek a a \( \tilde{b} \). Ve sklopení promítací roviny přímky a bude přímka \( \tilde{b} \) rovnoběžná s již sestrojenou přímkou (b). Odchylka přímek a a b v prostoru je rovna odchylce přímek (a) a (\( \tilde{b} \)). Protože jsou přímky (b) a (\( \tilde{b} \)) rovnoběžné, je odchylka přímek (a) a (\( \tilde{b} \)) rovna odchylce přímek (a) a (b). To znamená, že jsme nemuseli postupovat stejným postupem jako u obecných mimoběžných přímek, ale stačilo sklopit promítací roviny přímek a a b „na stejnou stranu“. Odchylka přímek a a b v prostoru se rovná odchylce přímek (a) a (b).
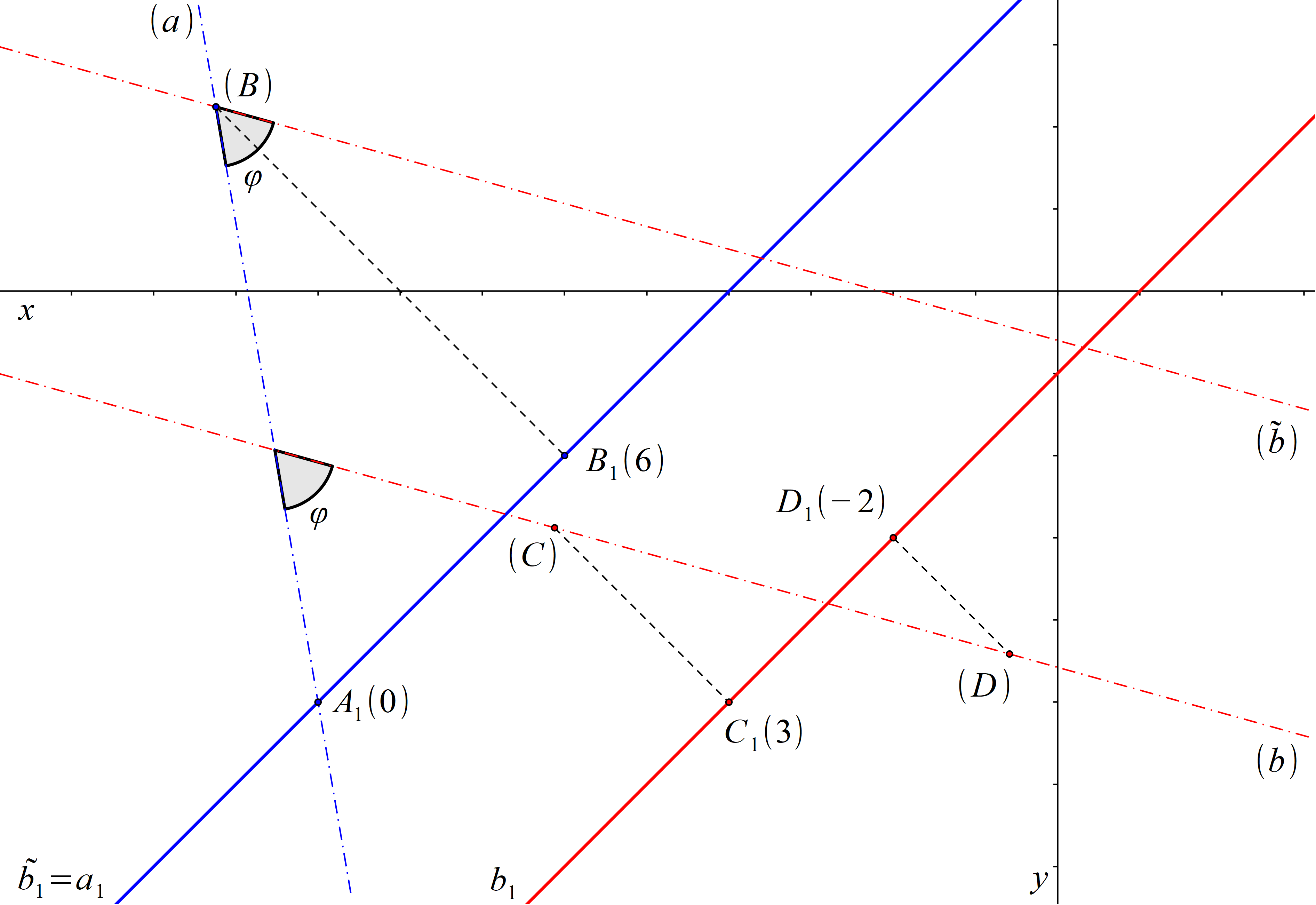
Obr. 59: Řešení příkladu 11.6
