Určete odchylku φ přímek a a b.

a = ↔AB, A = [−3; −2; 6], B = [−5; −3; 3]

b = ↔CD, C = [−2; −3; 1], D = [−8; −1; 6]

Řešení (obr. 61)

Nejprve určíme vzájemnou polohu přímek a a b. Průměty přímek a, b jsou různoběžné přímky. Přímky a, b tedy mohou být různoběžné nebo mimoběžné (viz kapitola Vzájemná poloha dvou přímek). Průsečík přímek a₁, b₁ je průmětem bodů E a F, kde E ∈ a a F ∈ b. Pokud mají body E, F stejnou kótu, splývají. Přímky a, b jsou potom různoběžné. V opačném případě jsou mimoběžné. Kóty bodů E, F zjistíme pomocí sklopení promítacích rovin přímek a, b. Průsečíkem kolmice vedené bodem E₁ k a₁ a přímky (a) je bod (E), průsečíkem kolmice vedené bodem F₁ k b₁ a přímky (b) je bod (F). Nyní vidíme, že z_E = |E₁(E)| > z_F = |F₁(F)|, což znamená, že přímky a, b jsou mimoběžné.

Dále proto vedeme libovolným bodem na přímce a přímku \( \tilde{b} \) rovnoběžnou s přímkou b. Veďme přímku \( \tilde{b} \) například bodem E. Přímky b a \( \tilde{b} \) potom leží v jedné promítací rovině a jejich průměty jsou totožné přímky. Odchylka φ mimoběžných přímek a a b je nyní rovna odchylce různoběžných přímek a a \( \tilde{b} \). Abychom určili odchylku přímek a a \( \tilde{b} \), otočíme rovinu α danou těmito dvěma přímkami do průmětny. K tomu potřebujeme sestrojit stopu roviny α. Stopa roviny α prochází stopníkem P^a přímky a a stopníkem \( P^\tilde{b} \) přímky \( \tilde{b} \). Stopník \( P^\tilde{b} \) určíme pomocí sklopení promítací roviny přímky \( \tilde{b} \). Přímka (\( \tilde{b} \)) prochází bodem (E) a je rovnoběžná s přímkou (b). Dále ve sklopení promítací roviny spádové přímky s^α roviny α procházející bodem E sestrojíme bod (E) a kružnici otáčení (k^E) bodu E, jejímž středem je stopník \( P^ {s^\alpha} \) přímky s^α a poloměrem vzdálenost bodu \( P^ {s^\alpha }\) od bodu (E). Bod E₀ je průsečíkem přímky \(s^\alpha_1 \) s kružnicí (k^E). Přímka a₀ je spojnicí bodu E₀ a bodu P^a. Přímka \( \tilde{b}_0 \) je spojnicí bodu E₀ a bodu \( P^\tilde{b} \). Odchylka φ přímek a a b v prostoru je rovna odchylce přímek a₀ a \( \tilde{b}_0 \).

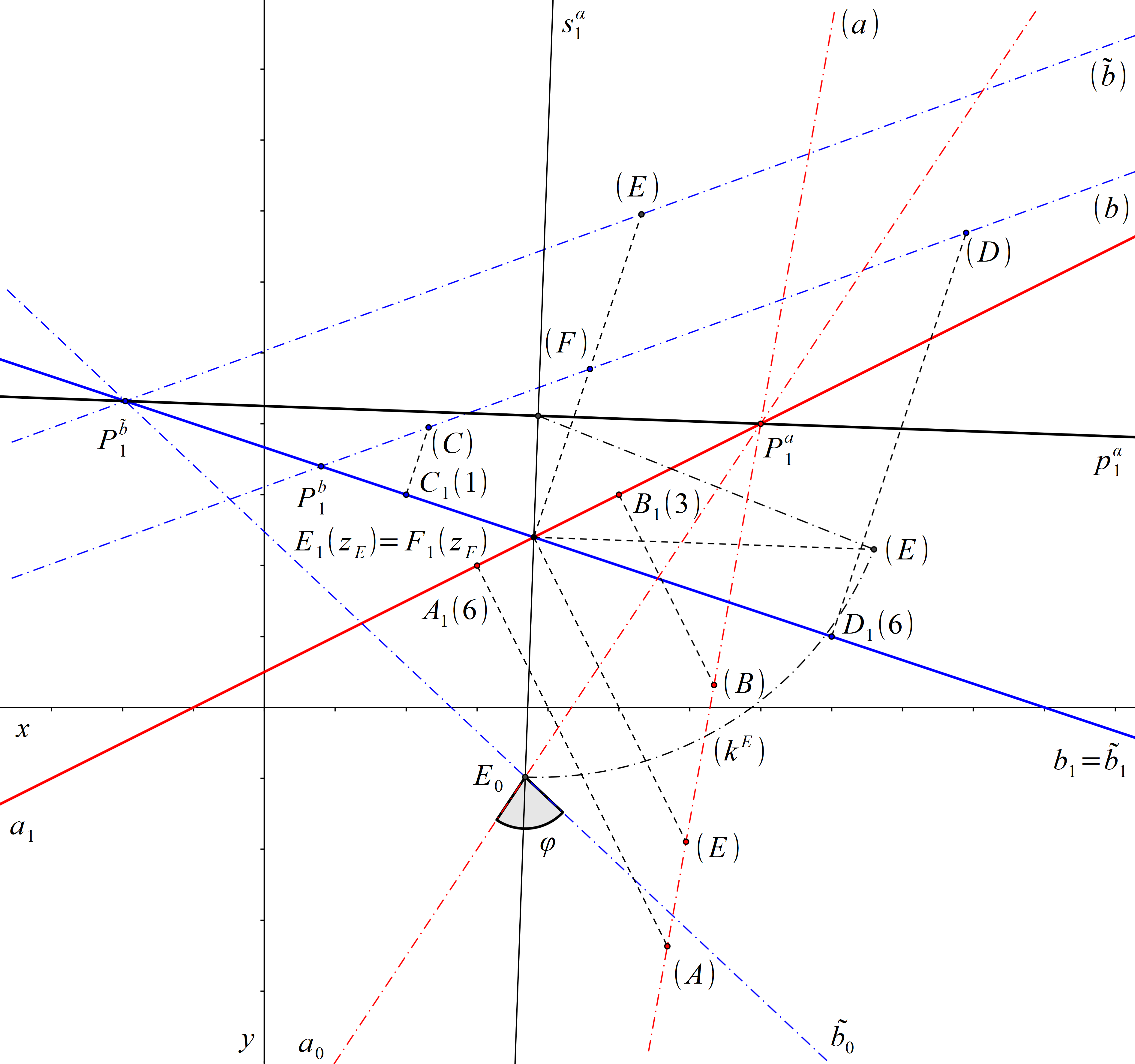
Obr. 61: Řešení příkladu 11.8

Předchozí příklad

Následující příklad

Teorie k příkladu