Zobrazte přímku a kolmou k rovině α procházející bodem A. Určete stopník kolmice a.
α = ↔ABC, A = [9; 3; 5], B = [7; 10; 0], C = [3; 2; 0]
Řešení (obr. 64)
Jelikož body B, C leží v průmětně, určují stopu roviny α. Jak již víme, přímka kolmá k rovině se promítá jako kolmice k hlavním přímkám roviny. Přímka a1 bude tedy procházet bodem A1 a bude kolmá ke stopě roviny α, čili splyne s průmětem \(s^\alpha_1 \) spádové přímky sα roviny α procházející bodem A. Stopník Pa přímky a dohledáme sklopením její promítací roviny. Nejprve ve sklopení sestrojíme spádovou přímku sα ležící v této rovině. Přímka (a) prochází bodem (A) a je na přímku (sα) kolmá. Stopník Pa přímky a je průsečíkem přímek a1 a (a).
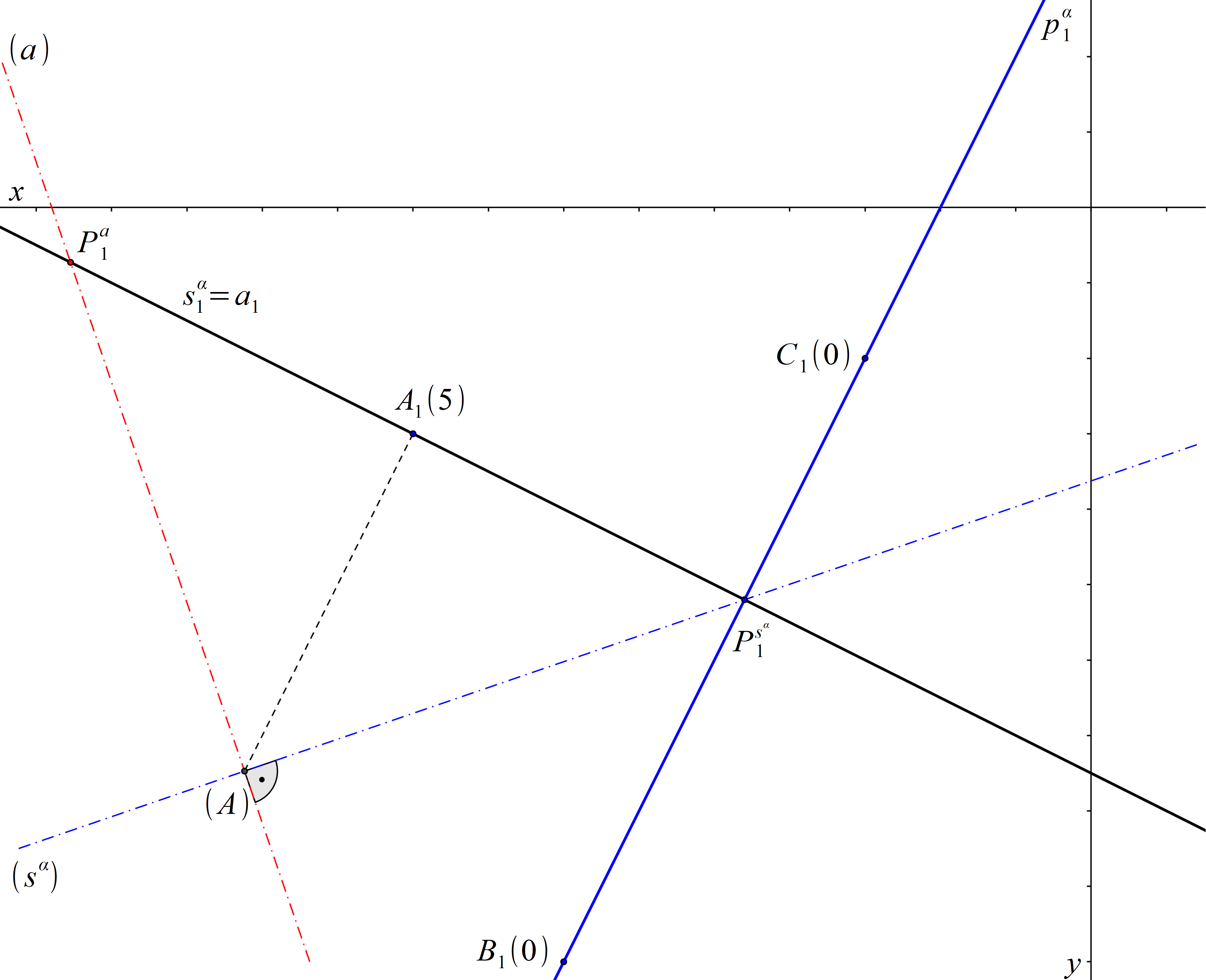
Obr. 64: Řešení příkladu 12.1
