Určete odchylku φ přímky a od roviny α.
α = ↔ABC, A = [8; 7; 0], B = [3; 2; 0], C = [8; 4; 3]
a = ↔DE, D = [8; 2; 2], E = [3; 7; 4]
Řešení (obr. 71)
Jelikož body A, B leží v průmětně, určují stopu roviny α. Rovina α není rovnoběžná s průmětnou a průmět a1 přímky a je kolmý ke stopě roviny α. Kolmým průmětem přímky a do roviny α bude tedy spádová přímka sα roviny α, která se promítá do totožné přímky s přímkou a1. Pro určení odchylky φ přímky a od roviny α stačí sklopit promítací rovinu přímky a. V tomto sklopení sestrojíme přímku a a přímku sα, a to pomocí bodu F o kótě 3 a stopníku \( P^ {s^\alpha }\). Hledaná odchylka φ je rovna odchylce přímek (a) a (sα).
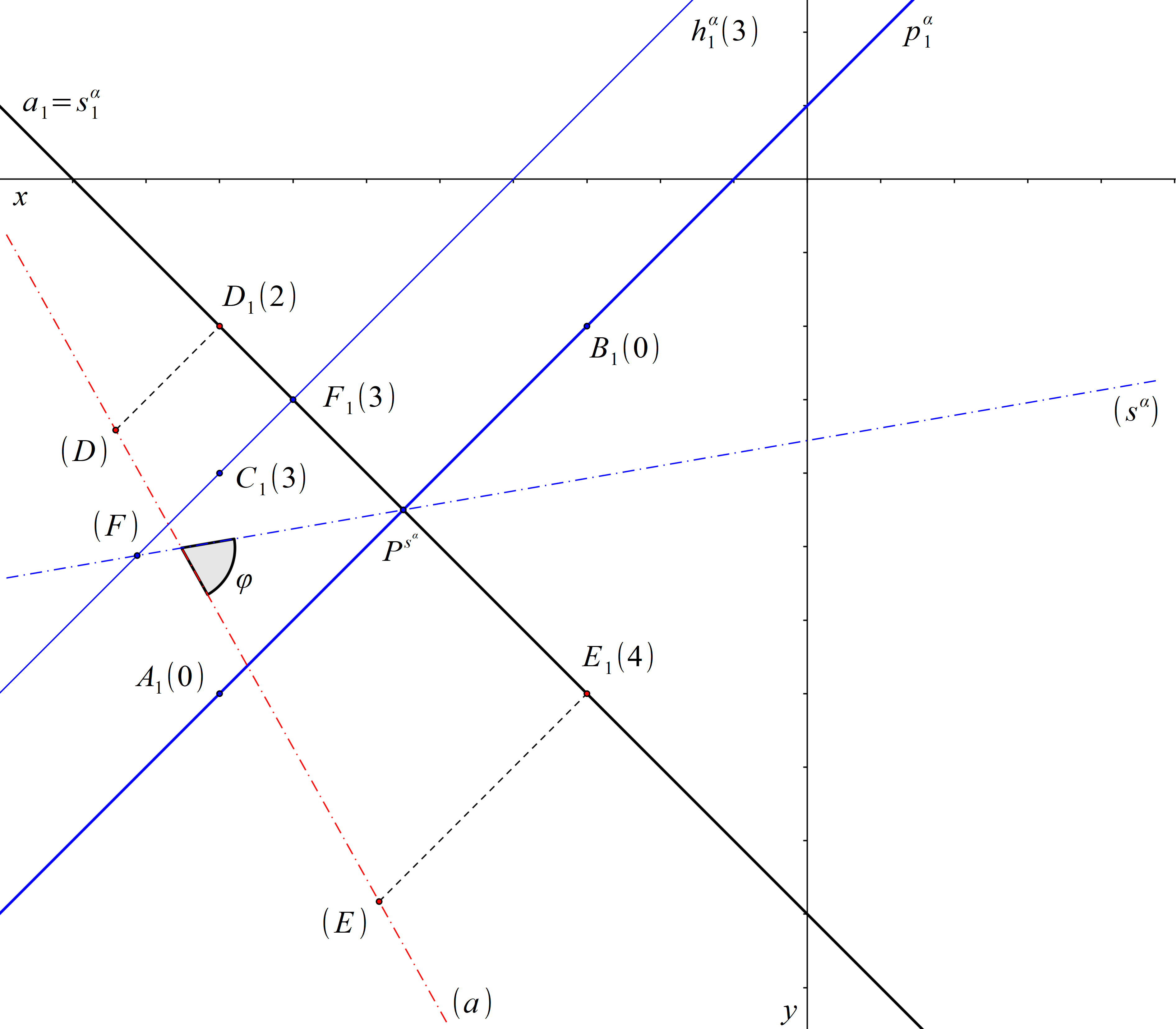
Obr. 71: Řešení příkladu 13.4
