Určete odchylku φ přímky a od roviny α.
α = ↔ABC, A = [11; 7; 0], B = [0; 5; 0], C = [0; 1; 3]
a = ↔DE, D = [4; 3; 2], E = [7; 5; 6]
Řešení (obr. 70)
Jelikož body A, B leží v průmětně, určují stopu roviny α. Rovina α není rovnoběžná s průmětnou a přímka a není kolmá k průmětně. Abychom určili odchylku φ přímky a a roviny α, sestrojíme pravoúhlý průmět \( \hat{a} \) přímky a do roviny α (viz příklad 12.4). Jedním bodem přímky \( \hat{a} \) bude průsečík F přímky a s rovinou α, který dohledáme analogickým způsobem jako v příkladu 6.1 pomocí krycí přímky m, která protíná hlavní přímku hα v bodě H o kótě 3 a jejíž stopník Pm leží na stopě roviny α. Dále vedeme bodem D kolmici b k rovině α. Přímka b1 prochází bodem D1 kolmo ke stopě pα roviny α. Ve sklopení promítací roviny přímky b sestrojíme spádovou přímku sα roviny α, která v této promítací rovině leží, a přímku b. Přímka (b) prochází bodem (D) a je kolmá k přímce (sα). Průsečík (G) přímek (sα) a (b) je sklopeným pravoúhlým průmětem G bodu D do roviny α. Bod G1 je patou kolmice vedené z bodu (G) na přímku b1. Body F a G určují přímku \( \hat{a} \), která je pravoúhlým průmětem přímky a do roviny α.
Hledaná odchylka φ přímky a od roviny α je nyní rovna odchylce přímek a a \( \hat{a} \). K dourčení odchylky φ už stačí jen rovinu β danou těmito dvěma přímkami otočit do průmětny. K tomu potřebujeme sestrojit stopu roviny β. Stopa roviny β prochází stopníkem Pa přímky a a stopníkem \( P^ {\hat {a} }\) přímky \( \hat{a} \). Stopník Pa najdeme pomocí sklopení promítací roviny přímky a. Jelikož přímka \( \hat{a} \) leží v rovině α, stopník \( P^ {\hat {a} }\) je průsečíkem přímek \(p^\alpha_1 \) a \( \hat{a}_1 \). V otočení roviny β konkrétně sestrojíme bod F konstrukcí znázorněnou na obr. 49. Přímka a0 prochází body F0 a Pa. Přímka \( \hat{a}_0 \) prochází body F0 a \( P^ {\hat {a} }\). Hledaná odchylka φ je rovna odchylce přímek a0 a \( \hat{a}_0 \).
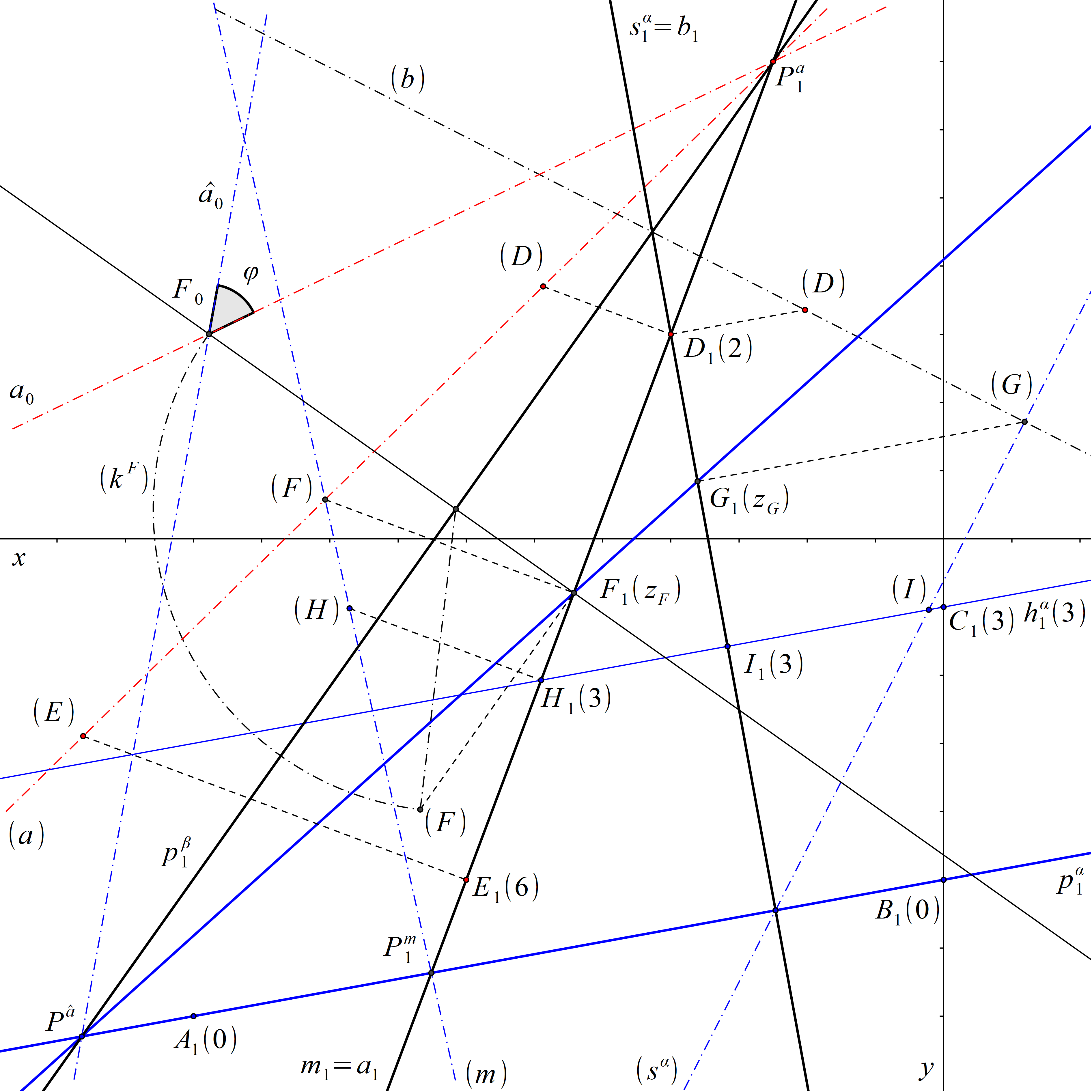
Obr. 70: Řešení příkladu 13.3
