Určete odchylku φ rovin α a β.

α = ↔ABC, A = [4; 10; 0], B = [−2; 8; 0], C = [4; 8; 4]

β = ↔DEF, D = [4; 3; 0], E = [7; 4; 0], F = [6; 6; 3]

Řešení (obr. 75)

Roviny α a β jsou obě různoběžné s průmětnou a jejich stopy jsou rovnoběžné. Proto sklopíme libovolnou promítací rovinu kolmou k oběma zadaným rovinám. V této promítací rovině leží spádová přímka s^α roviny α i spádová přímka s^β roviny β. Hledaná odchylka φ rovin α a β je rovna odchylce přímek (s^α) a (s^β).

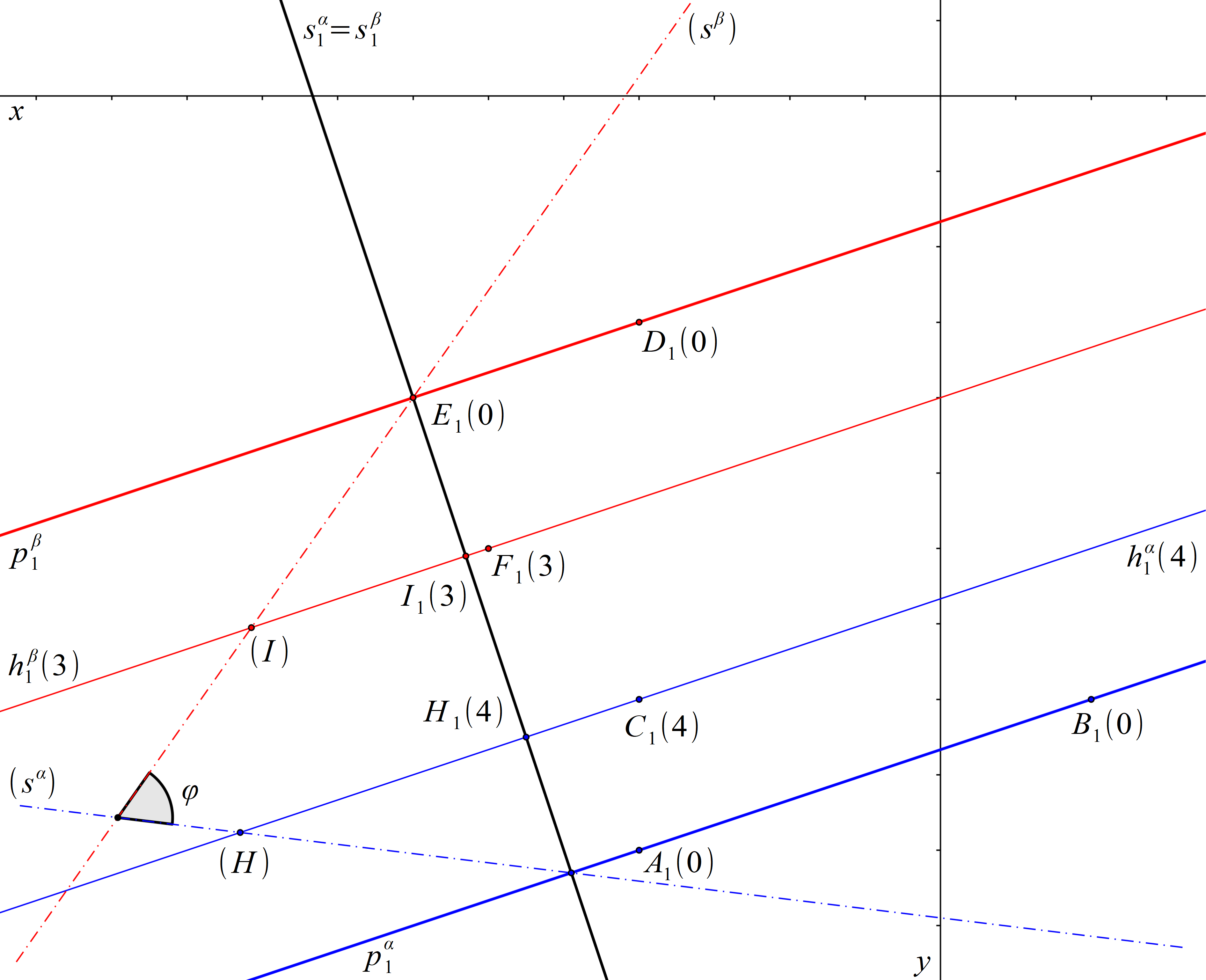
Obr. 75: Řešení příkladu 14.3

Krokovaná konstrukce

Předchozí příklad

Následující příklad

Teorie k příkladu