Určete odchylku φ rovin α a β.
α = ↔ABC, A = [8; 9; 0], B = [11; 5; 0], C = [4; 12; 1]
β = ↔DEF, D = [5; 8; 0], E = [3; 5; 0], F = [10; 10; 3]
Řešení – 1. způsob (obr. 73)
Roviny α a β jsou různoběžné s průmětnou a jejich stopy jsou různoběžné, proto sestrojíme průmět průsečnice c rovin α a β a libovolným bodem této průsečnice vedeme rovinu γ k ní kolmou. Dále zobrazíme průsečnici a rovin α a γ a průsečnici b rovin β a γ. Odchylka rovin α a β je rovna odchylce přímek a a b.
Jedním bodem průsečnice c je průsečík G stop pα a pβ. Jako druhý bod průsečnice c můžeme najít průsečík hlavních přímek o kótě 1. Průmětem hlavní přímky roviny α o kótě 1 je přímka vedená bodem C1 rovnoběžně se stopou roviny α. U roviny β najdeme hlavní přímku o kótě 1 například pomocí sklopení promítací roviny spádové přímky sβ procházející bodem E. Tuto promítací rovinu sklopíme pomocí bodu E a bodu H o kótě 3. Ve sklopení na spádové přímce najdeme bod I o kótě 1. Jeho průmětem vedeme rovnoběžku se stopou roviny β, která je průmětem hledané hlavní přímky roviny β o kótě 1. Spojnice průsečíku J hlavních přímek rovin α, β o kótě 1 a průsečíku G stop rovin α, β je průsečnice c rovin α, β.
Dále libovolným bodem K přímky c vedeme rovinu γ k ní kolmou (analogickým postupem jako v příkladu 12.2). Nejprve sklopíme promítací rovinu přímky c. Na přímce (c) zvolíme bod (K). Zvolme bod (K) například jako na obrázku. Ve sklopení promítací roviny přímky c dále sestrojíme spádovou přímkou sγ roviny γ, která v této promítací rovině leží. Přímka (sγ) prochází bodem (K) a je kolmá k přímce (c). Průsečík přímek (sγ) a \(s^\gamma_1 \) je stopníkem přímky sγ. Kolmice vedená tímto stopníkem k přímce \(s^\gamma_1 \) je stopou roviny γ. Průmět průsečnice a rovin α a γ prochází bodem K1 a průsečíkem Pa stop rovin α a γ. Průmět průsečnice b rovin β a γ prochází bodem K1 a průsečíkem Pb stop rovin β a γ. Odchylka rovin α a β je nyní rovna odchylce přímek a a b.
Rovinu γ, v níž přímky a a b leží, otočíme do průmětny. Konkrétně otočíme bod K konstrukcí znázorněnou na obr. 49. Přímka a0 prochází body K0 a Pa. Přímka b0 prochází body K0 a Pb. Hledaná odchylka φ je rovna odchylce přímek a0 a b0.
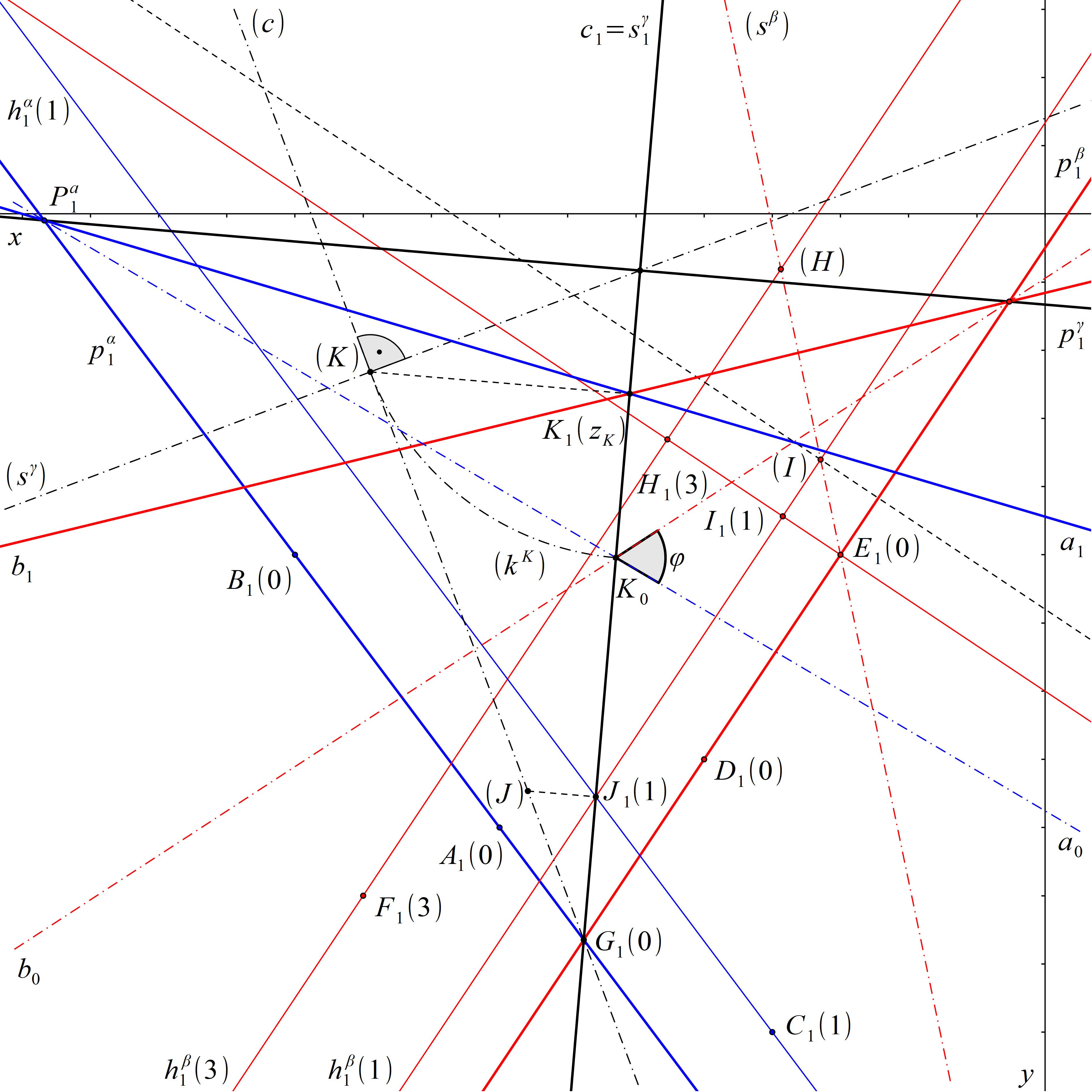
Obr. 73: Řešení příkladu 14.2 – 1. způsob
Řešení – 2. způsob (obr. 74)
Roviny α a β jsou různoběžné s průmětnou i navzájem. Zvolíme libovolný bod L a tímto bodem vedeme přímku a kolmou k rovině α a přímku b kolmou k rovině β (analogickým postupem jako v příkladu 12.1). Zvolme například L = [8; 1; 4]. Průmět a1 přímky a prochází bodem L1 kolmo ke stopě roviny α. Průmět b1 přímky b rovněž prochází bodem L1 a je kolmý ke stopě roviny β. Přímky a, b dourčíme například pomocí jejich stopníků Pa, Pb. Stopník Pa najdeme sklopením promítací roviny přímky a. Nejprve v tomto sklopení sestrojíme přímku sα, a to pomocí známého stopníku \( P^ {s^\alpha }\) a průsečíku G spádové přímky s hlavní přímkou roviny α o kótě 1. Přímka (a) prochází bodem (L) a je kolmá k přímce (sα). Stopník Pa je průsečíkem přímek (a) a \(s^\alpha_1 \). Stopník Pb najdeme analogicky sklopením promítací roviny přímky b.
Odchylka rovin α a β je nyní rovna odchylce přímek a a b. Abychom tuto odchylku určili, otočíme rovinu γ danou přímkami a a b do průmětny. K tomu potřebujeme sestrojit stopu roviny γ. Stopa roviny γ prochází stopníkem Pa přímky a a stopníkem Pb přímky b. Bod L otočíme konstrukcí znázorněnou na obr. 49. Přímka a0 prochází body L0 a Pa, přímka b0 prochází body L0 a Pb. Hledaná odchylka φ je rovna odchylce přímek a0 a b0.
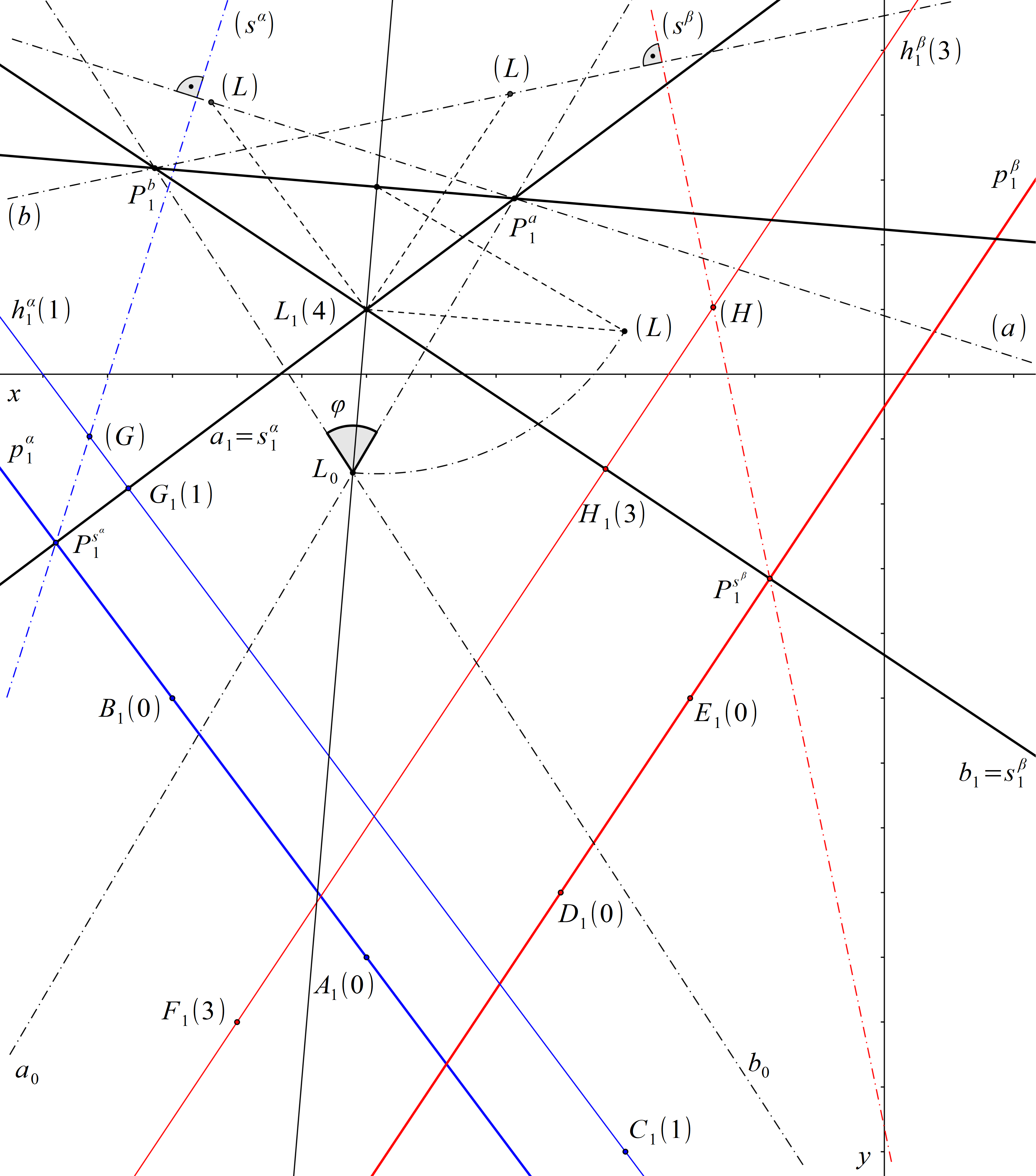
Obr. 74: Řešení příkladu 14.2 – 2. způsob
Závěr:
Oba uvedené postupy řešení jsou přibližně stejně náročné. Druhý způsob je naprosto univerzální, neboť jej můžeme aplikovat pro jakoukoli dvojici rovin. Oproti tomu první způsob lze použít jen pro různoběžné roviny.
