Určete vzdálenost bodu D = [7; 3; 3] od roviny α.
α = ↔ABC, A = [8; 0; 0], B = [2; 3; 0], C = [−2; 5; 2]
Řešení (obr. 79)
Jelikož body A, B leží v průmětně, určují stopu roviny α. Bod C1 leží na přímce \(p^\alpha_1 \), rovina α je tedy promítací. Kolmice a vedená bodem D k rovině α je rovnoběžná s průmětnou. Všechny body přímky a mají kótu 3, stejně jako bod D. Průmět přímky a prochází bodem D1 kolmo k přímce α1. Průsečík E přímky a a roviny α se promítne do průsečíku E1 přímek a1 a α1. Kóta bodu E je 3, protože bod E je bodem přímky a. Vzdálenost bodu D od roviny α je nyní rovna vzdálenosti bodů D a E. Poněvadž je kóta bodů D a E stejná, je hledaná vzdálenost rovna vzdálenosti bodů D1 a E1.
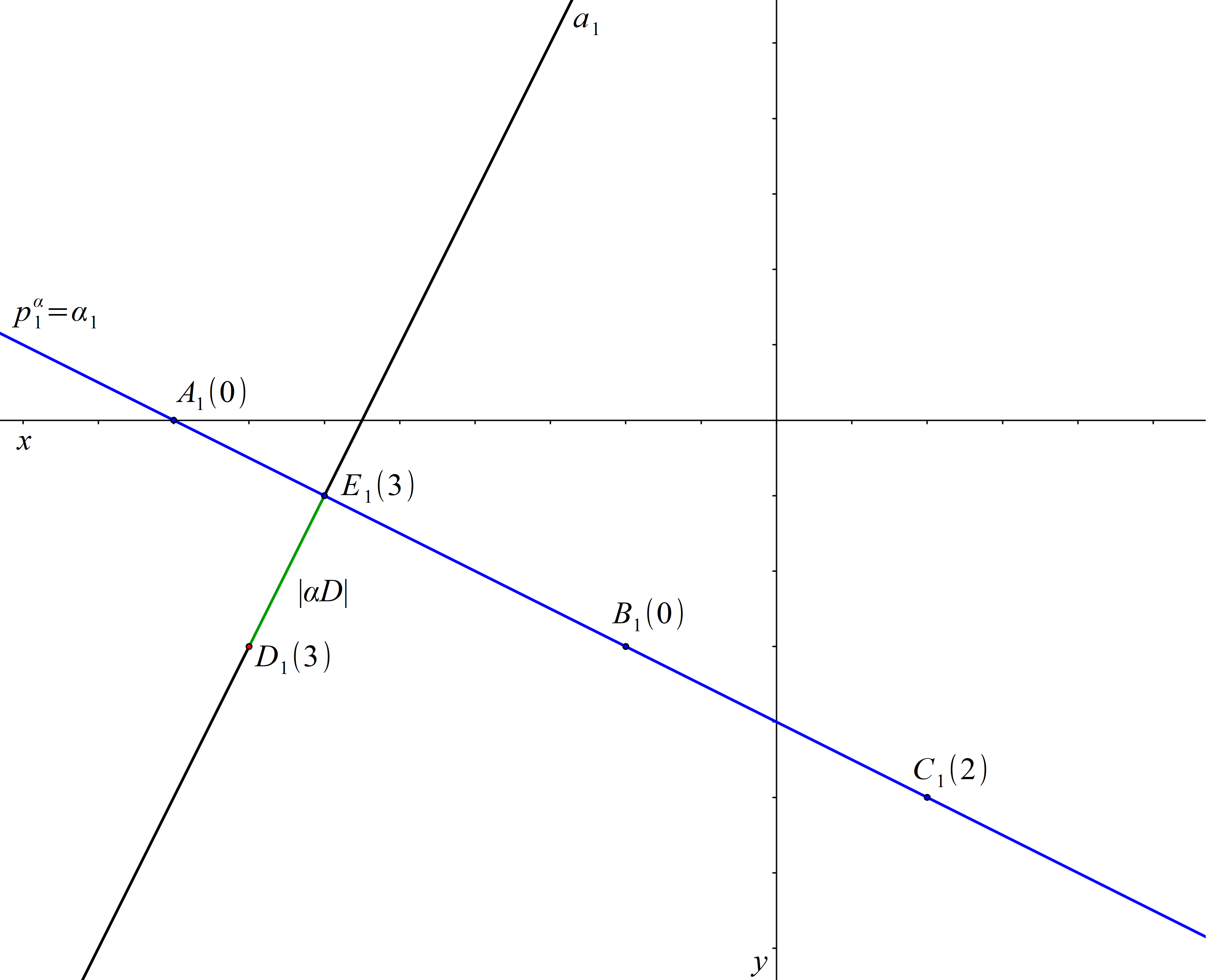
Obr. 79: Řešení příkladu 16.1
