Přesvědčte se, že je přímka a rovnoběžná s rovinou α, a určete vzdálenost přímky a a roviny α.
α = ↔ABC, A = [3; 3; 0], B = [−2; −1; 0], C = [7; 2; 4]
a = ↔DE, D = [8; 5; 3], E = [−2; −3; 3]
Řešení (obr. 84)
Body A, B leží v průmětně, proto určují stopu roviny α. Přímka \(h^\alpha_1 \) rovnoběžná se stopou roviny α vedená bodem C1 je průmětem hlavní přímky hα roviny α o kótě 4. Přímka a je rovnoběžná s pα, protože body D a E mají navzájem stejnou kótu a přímka a1 je rovnoběžná s \(p^\alpha_1 \). Přímka a a rovina α jsou tedy rovnoběžné (viz kapitola Vzájemná poloha přímky a roviny).
Vzdálenost roviny α a přímky a je rovna vzdálenosti libovolného bodu přímky a od roviny α. Určeme nyní hledanou vzdálenost jako vzdálenost bodu D od roviny α. Bodem D vedeme kolmici b k rovině α a najdeme průsečík G přímky b s rovinou α. Hledaná vzdálenost je rovna délce úsečky DG. Přímka b1 prochází bodem D1 kolmo ke stopě roviny α a splývá s průmětem \(s^\alpha_1 \) spádové přímky sα roviny α. Promítací rovinu přímek b a sα sklopíme. Sestrojíme přímku (sα), a to pomocí známého stopníku a průsečíku F s hlavní přímkou o kótě 4. Dále v tomto sklopení sestrojíme přímku (b) jako kolmici vedenou bodem (D) k přímce (sα). Průsečík (G) přímek (b) a (sα) je sklopeným průsečíkem G přímky b a roviny α. Hledaná vzdálenost roviny α a přímky a je rovna délce úsečky (D)(G).
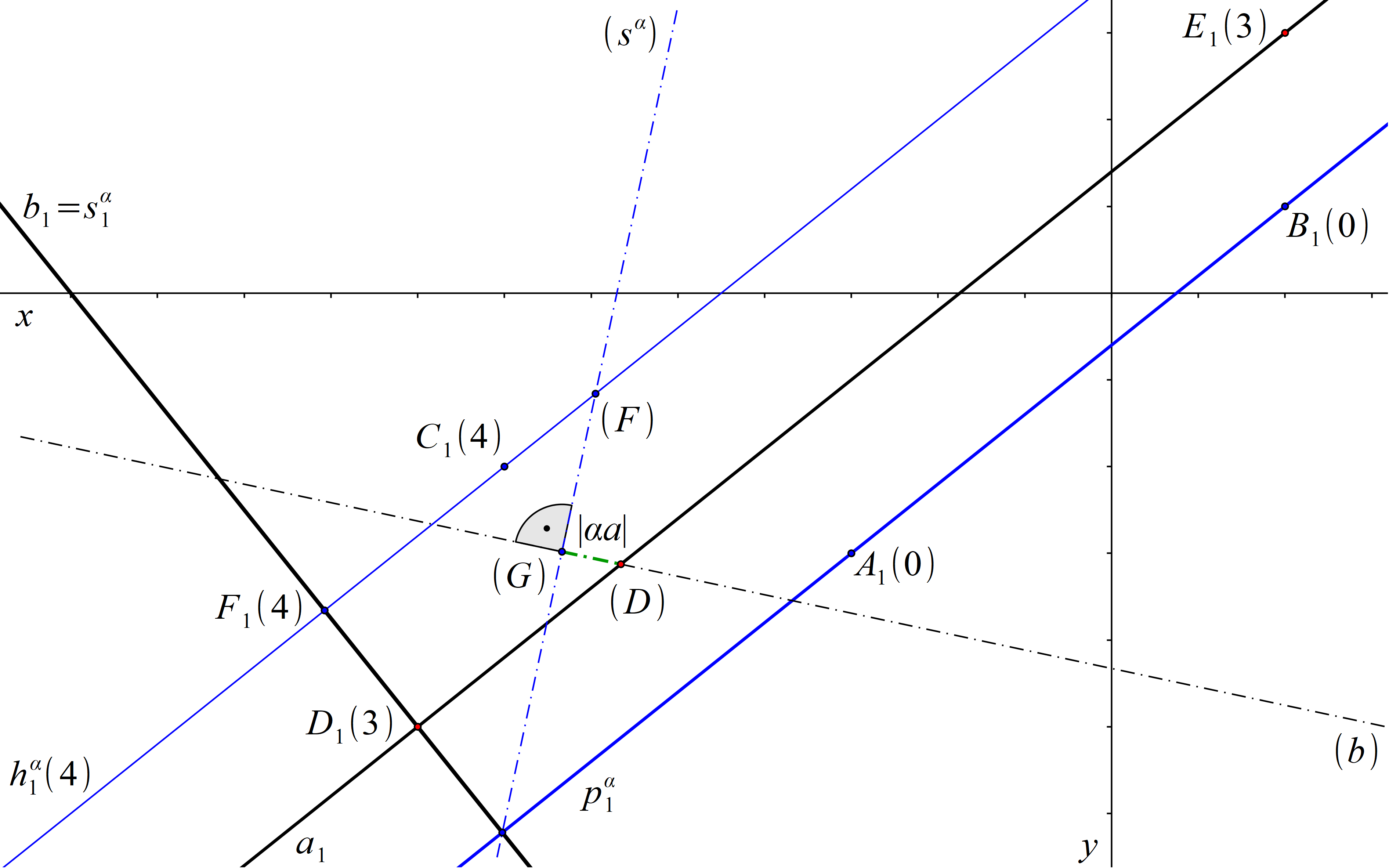
Obr. 84: Řešení příkladu 16.6
