Přesvědčte se, že je přímka a rovnoběžná s rovinou α, a určete vzdálenost přímky a a roviny α.

α = ↔ABC, A = [8; 4; 0], B = [7; 3; 0], C = [3; −1; 3]

a = ↔DE, D = [5; 5; 2], E = [3; 3; 4]

Řešení (obr. 85)

Rovina α je promítací a promítá se do rovnoběžné přímky s průmětem a₁ přímky a. Z toho plyne, že rovina α a přímka a jsou rovnoběžné (viz kapitola Vzájemná poloha přímky a roviny).

Abychom určili vzdálenost roviny α a přímky a, vedeme libovolným bodem přímky a kolmici b k rovině α. Veďme přímku b například bodem E. Vzdálenost roviny α a přímky a je nyní rovna vzdálenosti bodu E od průsečíku F přímky b s rovinou α. Protože je rovina α promítací a přímka b je k rovině α kolmá, je přímka b rovnoběžná s průmětnou. Délka úsečky EF je tedy rovna délce úsečky E₁F₁.

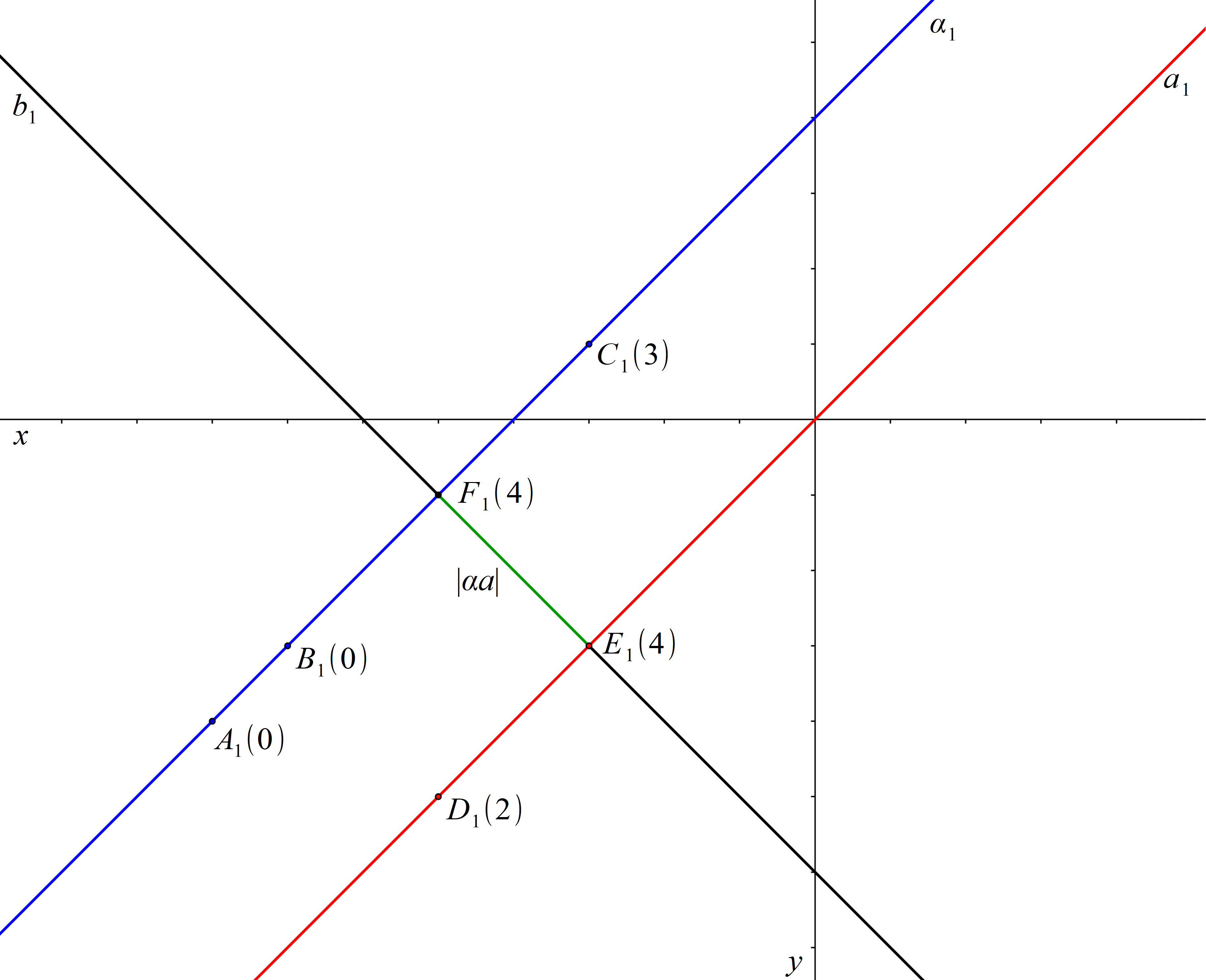
Obr. 85: Řešení příkladu 16.7

Předchozí příklad

Následující příklad

Teorie k příkladu