Určete vzdálenost bodu C = [2; −5; 6] od přímky a.
a = ↔AB, A = [5; −1; 5], B = [2; −3; 3]
Řešení – 1. způsob (obr. 86)
Abychom zjistili vzdálenost bodu C a přímky a, proložíme bodem C rovinu α kolmou k přímce a. Hledaná vzdálenost je rovna vzdálenosti bodu C od průsečíku E přímky a a roviny α. Rovnoběžka vedená bodem C1 kolmo k přímce a1 je průmětem hlavní přímky roviny α o kótě 6. Průsečík přímek a1 a \(h^\alpha_1 \) je průmětem bodu D o kótě 6, který leží v rovině α i v promítací rovině přímky a. Dále sklopíme promítací rovinu přímky a. V tomto sklopení sestrojíme přímku a a spádovou přímku sα roviny α, která v této promítací rovině leží. Přímka (sα) prochází bodem (D) a je kolmá k přímce (a). Průsečík přímek (a) a (sα) je sklopeným průsečíkem E přímky a s rovinou α. Bod E1 je patou kolmice vedené z bodu (E) na přímku a1. Kóta zE bodu E je kladná a je rovna vzdálenosti bodů (E) a E1. Vzdálenost bodu C od přímky a je nyní rovna vzdálenosti bodů C a E. Abychom tuto vzdálenost určili, sklopíme promítací rovinu úsečky CE. Hledaná vzdálenost bodu C od přímky a je rovna vzdálenosti bodů (C) a (E).
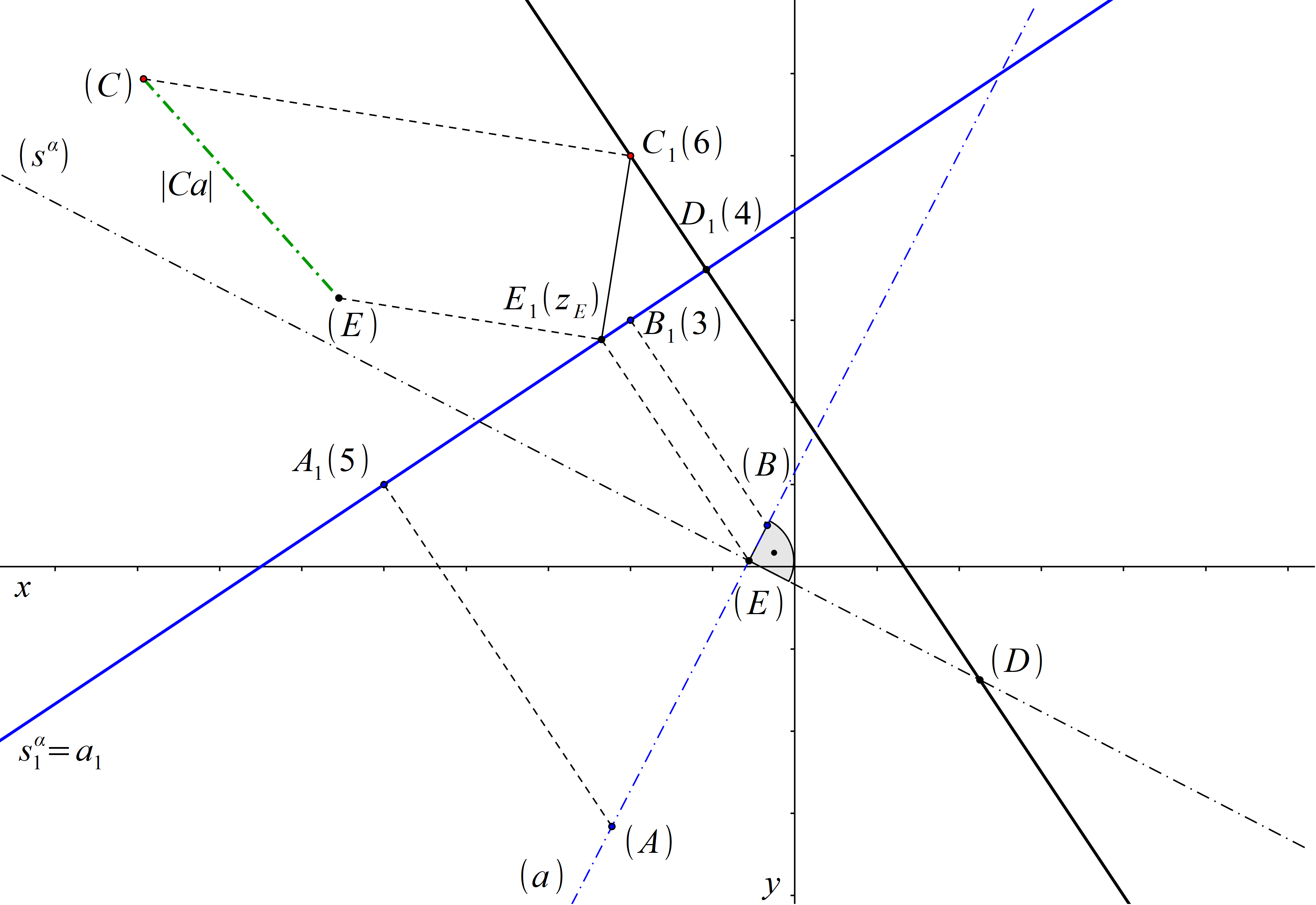
Obr. 86: Řešení příkladu 17.1 – 1. způsob
Řešení – 2. způsob (obr. 87)
Tento příklad rovněž můžeme řešit otočením roviny β = ↔ABC do průmětny, k čemuž budeme potřebovat stopu roviny β. Jedním bodem stopy pβ roviny β je stopník Pa přímky a. Jako druhý bod najdeme stopník PBC přímky BC sklopením promítací roviny přímky BC.
Dále konstrukcí znázorněnou na obrázku 49 sestrojíme bod C0. Otočíme také přímku a. Přímka a0 prochází body B0 a Pa. Bod B0 najdeme pomocí osové afinity, je průsečíkem přímek C0PBC a průmětu \( {}^1 s^\beta_1 \) spádové přímky \({}^1 s^\beta_1 \) roviny β procházející bodem B. Hledanou vzdálenost bodu C od přímky a nyní vidíme v otočení jako vzdálenost bodu C0 od přímky a0.
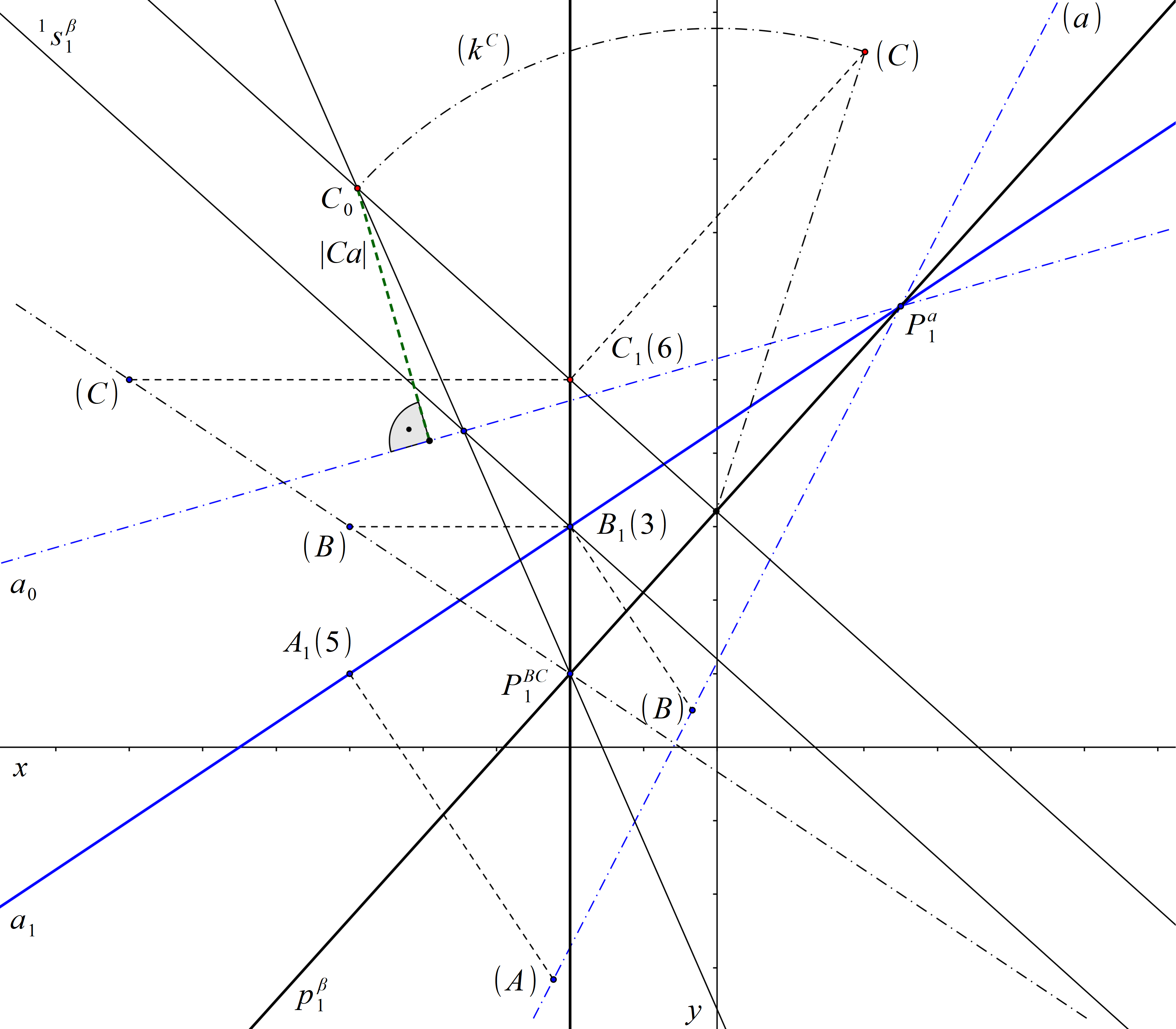
Obr. 87: Řešení příkladu 17.1 – 2. způsob
Závěr:
Druhý uvedený způsob řešení je konstrukčně pracnější. Oba postupy jsou naprosto univerzální, můžeme je aplikovat při jakémkoli zadání bodu a přímky.
