Přesvědčte se, že jsou přímky a a b mimoběžné, a určete jejich vzdálenost.
a = ↔AB, A = [−3; 1; 6], B = [−7; −3; 3]
b = ↔CD, C = [−2; −3; 1], D = [−8; 2; 4]
Řešení (obr. 94)
Průměty přímek a, b jsou různoběžné přímky. Přímky a, b tedy mohou být různoběžné nebo mimoběžné (viz příklad 4.1). Průsečík přímek a1, b1 je průmětem bodů E a F, kde E ∈ a a F ∈ b. Pokud mají body E, F stejnou kótu, jsou totožné. Přímky a, b jsou potom různoběžné. V opačném případě jsou mimoběžné. Kóty bodů E, F zjistíme pomocí sklopení promítacích rovin přímek a, b. Vidíme, že zE = |E1(E)| > zF = |F1(F)|, což znamená, že přímky a, b jsou mimoběžné.
Abychom zjistili vzdálenost přímek a a b, proložíme přímkou a rovinu α rovnoběžnou s přímkou b. Vzdálenost přímek a a b je rovna vzdálenosti libovolného bodu přímky b od roviny α. Rovina α je jednoznačně určena přímkou a a přímkou \( \tilde{b} \) vedenou libovolným bodem přímky a rovnoběžně s přímkou b. Veďme přímku \( \tilde{b} \) například bodem E. Přímky b a \( \tilde{b} \) potom leží v jedné promítací rovině a jejich průměty b1, \( \tilde{b}_1 \) jsou totožné přímky. Sestrojíme stopu roviny α, která je spojnicí stopíků Pa přímky a a \( P^\tilde{b} \) přímky \( \tilde{b} \). Jedním bodem stopy roviny α je stopním Pa přímky a. Dalším bodem stopy roviny α je stopník \( P^\tilde{b} \) přímky \( \tilde{b} \), který určíme sklopením promítací roviny přímek b a \( \tilde{b} \). Přímka (\( \tilde{b} \)) je rovnoběžná s přímkou (b) a prochází bodem (B).
Vzdálenost přímek a, b je nyní rovna vzdálenosti libovolného bodu přímky b, například bodu F, od roviny α. Abychom zjistili vzdálenost bodu F od roviny α (viz př. 12.3), najdeme pravoúhlý průmět G bodu F do roviny α. Bod G je patou kolmice c vedené bodem F k rovině α. Přímka c1 prochází bodem F1 kolmo ke stopě roviny α a splývá s průmětem \(s^\alpha_1 \) spádové přímky sα roviny α. Ve sklopení promítací roviny přímek c a sα sestrojíme přímku (sα) pomocí známého stopníku \( P^ {s^\alpha }\) a bodu E. Dále v tomto sklopení sestrojíme přímku c. Přímka (c) prochází bodem (F) a je kolmá k přímce (sα). Průsečík přímek (sα) a (c) je sklopeným pravoúhlým průmětem G bodu F do roviny α. Hledaná vzdálenost bodu F od roviny α je rovna vzdálenosti bodů (F) a (G).
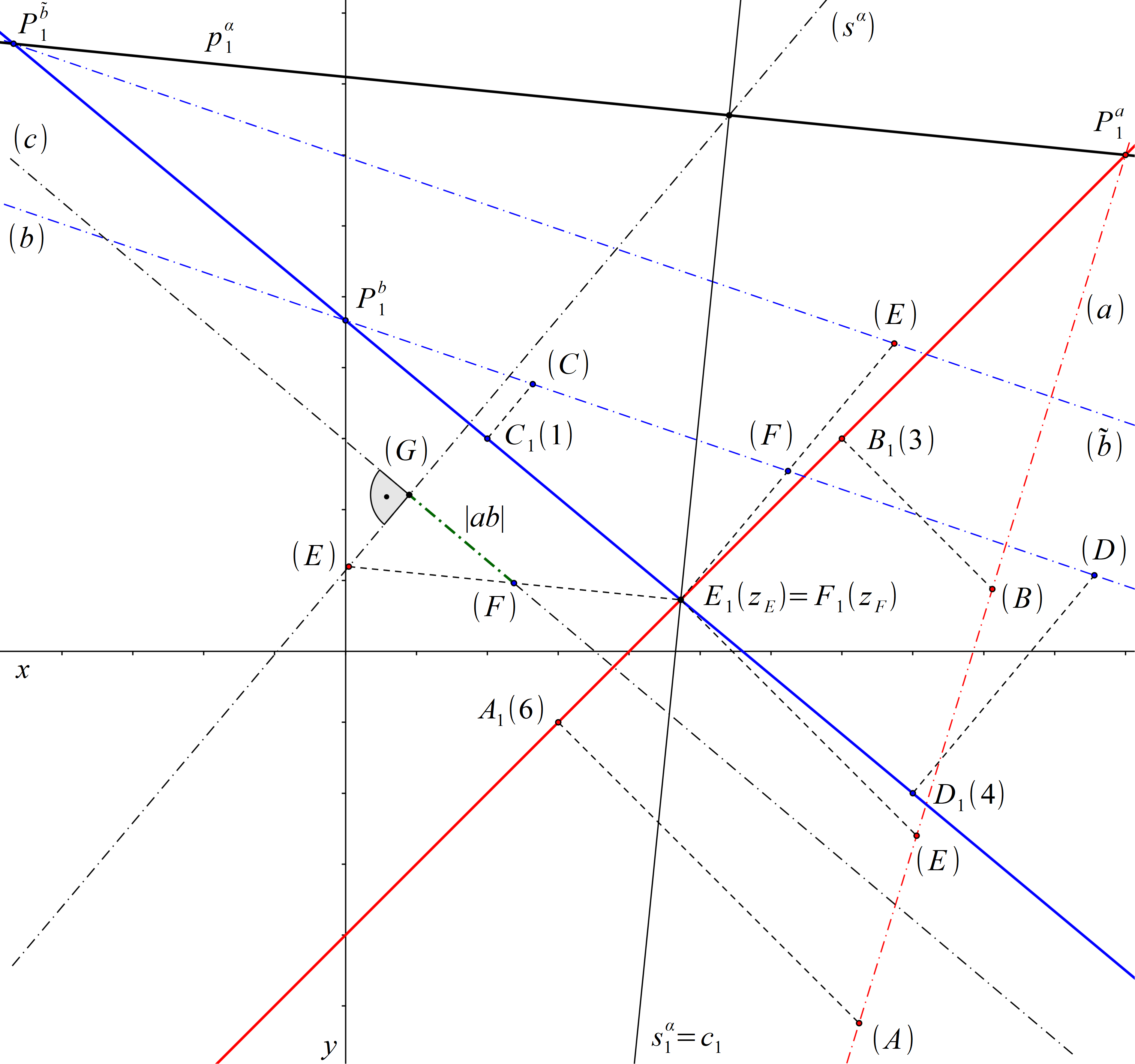
Obr. 94: Řešení příkladu 18.2
